AHA'S BOOK

在文章 数据结构算法之 Dijkstra 单源最短路径（原理部分）中，给出了 Dijkstra 算法求单源最短路径的图文步骤，本文将给出该算法的代码实现。

Dijkstra 算法步骤

回顾一下 数据结构算法之 Dijkstra 单源最短路径（原理部分）中给出的 Dijkstra 算法的具体步骤：

  1. 创建一个距离数组dist[]，用于存储源节点到各个节点的最短路径长度。初始时，将源节点的距离设为 0，与源节点直接相连的节点的距离设为边的权重，其他节点的距离设为无穷大。
  2. 创建一个标记数组visited[]，用于标记是否已经访问过该节点。初始时，将源节点标记为已访问，其他节点标记为未访问。
  3. 以源节点为基准，遍历所有与其相邻的、未访问过的节点，计算「源节点」到这些相邻节点的距离，并从未访问的节点中选择距离「源节点」最近的节点，作为基准节点。
  4. 以这个基准节点为中间节点，更新从源节点经过中间节点到达其它节点的距离到 dist[] 数组中，并将这个基准节点标记为已访问。
    • 更新的方式是：如果「从新的中间节点」到「该节点」的距离小于原本到它的距离，则更新它的值（你要从这个节点走才更近哦），并将这个中间节点作为它的前驱节点。
  5. 重复步骤 3 和步骤 4，直到所有节点都被访问过。
  6. 最终，dist[]数组中存储的就是源节点到其他所有节点的最短路径长度。

步骤三中的「相邻」节点包括直接与源节点相邻、通过已访问的节点间接与源节点相邻这两大类。换句话说，也就是 dist[] 数组中只要不是无穷大，就与源节点直接或间接相邻。

Dijkstra 算法实现

定义图结构

1
2
3
4
5
6
7
// 邻接矩阵
typedef struct _graph {
    char vexs[MAX];        // 顶点集合
    int vexnum;            // 顶点数
    int edgenum;           // 边数
    int matrix[MAX][MAX];  // 邻接矩阵
} Graph;

Graph 是图的邻接矩阵对应的结构体：

  • vexs 用于保存顶点的集合，vexnum 是顶点数量，edgenum 是边数；
  • matrix 用于保存邻接点信息的二维数组，matrix[i][j] 表示顶点 vexs[i] 和顶点 vexs[j] 之间的边的权重，若 matrix[i][j] = INF，则表示这两个顶点之间没有边（不是邻接点）。

定义边结构

实际中，一般给出的信息都是哪两个顶点之间有边，边的权重是多少，所有我们给出一个结构体用于存储边的数据。

1
2
3
4
5
6
// 边的结构体
typedef struct _edgeData {
    char start;  // 边的起点
    char end;    // 边的终点
    int weight;  // 边的权重
} EData;

在编码中，图结构体变量的数据将会从边结构体变量的数据中获取。

获取顶点的索引

这里的顶点是字符型（而非整数型），所以需要获取字符型顶点对应的索引——它在顶点集合中的位置。这样，才方便后续将邻接点存储在图结构的成员 matrix 中。

1
2
3
4
5
6
7
8
9
// 获取顶点在顶点集合中的索引
int getIndexOfVex(Graph *pGraph, char vex) {
    for (int i = 0; i < pGraph->vexnum; i++) {
        if (pGraph->vexs[i] == vex) {
            return i;
        }
    }
    return -1;
}

构建图数据

就像上面说的，图结构体变量的数据将会从边结构体变量的数据中获取。所以，我们在这里实现了从给定的边数据来初始化图数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 构建图
void createGraph(Graph *pGraph, char vexs[], int vexnum, EData edges[], int edgenum) {
    // 初始化顶点数、边数、顶点集合
    pGraph->vexnum = vexnum;
    pGraph->edgenum = edgenum;
    memcpy(pGraph->vexs, vexs, vexnum * sizeof(char));

    // 初始化邻接矩阵
    for (int i = 0; i < pGraph->vexnum; i++) {
        for (int j = 0; j < pGraph->vexnum; j++) {
            pGraph->matrix[i][j] = (i == j ? 0 : INF);
        }
    }

    // 添加边数据到图中
    for (int i = 0; i < pGraph->edgenum; i++) {
        // 这里要保证顶点的索引有效
        int start = getIndexOfVex(pGraph, edges[i].start);
        int end = getIndexOfVex(pGraph, edges[i].end);
        int weight = edges[i].weight;
        pGraph->matrix[start][end] = weight;
        pGraph->matrix[end][start] = pGraph->matrix[start][end];  // 无向图加这行，有向图不加这行
    }
}

对于无向图，要多加一行代码 pGraph->matrix[end][start] = pGraph->matrix[start][end] 哦。

Dijkstra 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// Dijkstra 算法，找到源顶点到各顶点的最短路径
void dijkstra(Graph *pGraph, char start, int dist[], int prev[]) {
    int i, j, k;
    int visited[MAX]; // 标记顶点是否已被访问

    int startIdx = getIndexOfVex(pGraph, start);

    // 步骤一 & 二：初始化访问数组、距离数组、路径数组
    for (i = 0; i < pGraph->vexnum; i++) {
        visited[i] = 0; // 顶点未被访问
        dist[i] = pGraph->matrix[startIdx][i]; // 初始化源顶点到各顶点的距离
        prev[i] = (dist[i] != INF ? startIdx : -1); // 如果源顶点到该顶点有边，则设置前驱顶点为源顶点
    }
    visited[startIdx] = 1; // 源顶点已被访问
    prev[startIdx] = -1;  // 源顶点没有前驱顶点

    // 步骤五：遍历 N-1 次，每次找到一个顶点的最短路径
    for (i = 1; i < pGraph->vexnum; i++) {
        int min = INF;
        
        // 步骤三：找到未被访问的顶点中距离最小的顶点 k
        for (j = 0; j < pGraph->vexnum; j++) {
            if (!visited[j] && dist[j] < min) {
                min = dist[j];
                k = j;
            }
        }

        // 步骤四：更新 dist 数组和 prev 数组
        for (j = 0; j < pGraph->vexnum; j++) {
            int distk2j = min + pGraph->matrix[k][j]; // 溢出风险, 所以定义的 INF 为一半的最大值
            // 如果「从新的中间节点」到「该节点」的距离小于原本到它的距离，则更新它的值
            if (!visited[j] && distk2j < dist[j]) {
                dist[j] = distk2j;
                prev[j] = k;
            }
        }
        visited[k] = 1; // 将基准节点标记为已访问
    }
}

一次遍历可以访问一个顶点，源节点在初始化时被访问；所以，遍历 N-1 次后，所有顶点就都被访问过了。

打印最短路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 打印给定起点和终点的最短路径
void printPath(Graph *pGraph, char start, char end, int dist[], int prev[]) {
    int startIdx = getIndexOfVex(pGraph, start);
    int endIdx = getIndexOfVex(pGraph, end);

    int i = endIdx, count = 0;
    char path[MAX];

    // 逆序将路径顶点存入 path 数组
    while (i != startIdx) {
        path[count++] = pGraph->vexs[i];
        i = prev[i];  // 顶点 i 的前驱顶点
    }

    // 打印路径顶点
    printf("%c -> %c: %c", pGraph->vexs[startIdx], pGraph->vexs[endIdx], pGraph->vexs[startIdx]);
    for (i = count - 1; i >= 0; i--) {
        printf(" %c", path[i]);
    }
    printf(", minDist: %d\n", dist[endIdx]);
}

Dijkstra 算法测试

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>
#include <string.h>

#define MAX (100)
#define INF ((~(0x1U << 31)) >> 1) // 最大值 0X7FFFFFFF 的一半

typedef struct _graph {
    char vexs[MAX];        // 顶点集合
    int vexnum;            // 顶点数
    int edgenum;           // 边数
    int matrix[MAX][MAX];  // 邻接矩阵
} Graph;

typedef struct _edgeData {
    char start;  // 边的起点
    char end;    // 边的终点
    int weight;  // 边的权重
} EData;

int getIndexOfVex(Graph *pGraph, char vex);
void createGraph(Graph *pGraph, char vexs[], int vexnum, EData edges[], int edgenum);
void dijkstra(Graph *pGraph, char start, int dist[], int prev[]);
void printPath(Graph *pGraph, char start, char end, int dist[], int prev[]);

int main() {
    char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
    int vexnum = sizeof(vexs) / sizeof(vexs[0]);
    EData edges[] = {
        {'A', 'B', 2},
        {'A', 'C', 6},
        {'B', 'D', 5},
        {'C', 'D', 8},
        {'D', 'F', 15},
        {'D', 'E', 10},
        {'E', 'F', 6},
        {'F', 'G', 6},
        {'E', 'G', 2}};
    int edgenum = sizeof(edges) / sizeof(edges[0]);
    Graph graph;
    int dist[MAX]; // 存储最短路径长度
    int prev[MAX]; // 存储前驱节点

    createGraph(&graph, vexs, vexnum, edges, edgenum);
    dijkstra(&graph, 'A', dist, prev);
    for (int i = 0; i < vexnum; i++) {
        printPath(&graph, 'A', vexs[i], dist, prev);
    }

    return 0;
}

一个数加上无穷大会溢出，所以定义的 INF 为最大值的一半，防止溢出风险。

测试结果

这是测试用例中构建的图：

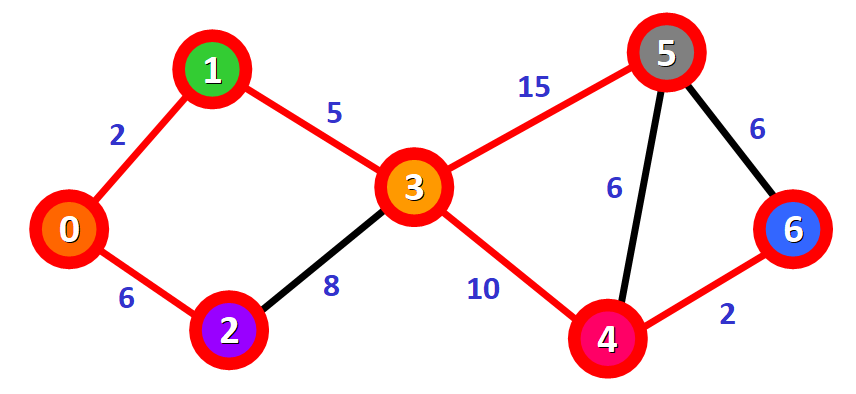
测试结果，打印从起点到终点的最短路径上的节点和最短距离：

1
2
3
4
5
6
7
A -> A: A, minDist: 0
A -> B: A B, minDist: 2
A -> C: A C, minDist: 6
A -> D: A B D, minDist: 7
A -> E: A B D E, minDist: 17
A -> F: A B D F, minDist: 22
A -> G: A B D E G, minDist: 19

参考资料：

  1. https://www.cnblogs.com/skywang12345/p/3711512.html
aha
2023-11-21
数据结构 图算法
Expand all Back to top Go to bottom Search in blogs
银河白
豆沙绿
杏仁黄
青草绿
秋叶褐