LeetCode 刷题

142 环形链表 II：给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。说明：不允许修改给定的链表。

1
2
3
4
5
6
7
8
9
10
11

输入: head = [3,2,0,-4], pos = 1
输出: 返回索引为 1 的链表节点 
解释: 链表中有一个环，其尾部连接到第二个节点。

输入: head = [1,2], pos = 0
输出: 返回索引为 0 的链表节点 
解释: 链表中有一个环，其尾部连接到第一个节点。

输入: head = [1], pos = -1
输出: 返回 null 
解释: 链表中没有环。

哈希表 + 遍历

我们可以借助一个哈希表来存储链表中的节点，随着遍历的进行，会第二次遇到相同的节点，这个最先遇到的节点就是入环的第一个节点。

时间复杂度：O(n)，一趟遍历，空间复杂度：O(n)，哈希表最多存储链表的全部节点。

快慢指针

前置知识：使用快慢指针可以判断链表中是否存在环。若存在环，则快慢指针终有相遇的时候，若不存在环，快指针最后会退出链表。

因此，判断环形链表入环的第一个节点，也可以使用快慢指针。

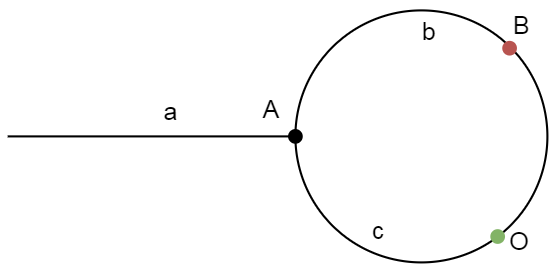
如上图，当快慢指针在位置 $O$ 相遇时，假设快指针绕环走过 $n$ 圈，那么其走过链表的总长度为 $a + b + n(b + c)$。同样地，慢指针绕环走过 $m$ 圈，那么其走过链表的总长度为 $a + b + m(b + c)$。

假设快指针每次走 $2$ 步，慢指针每次走 $1$ 步，那么有 $a + b + n(b + c) = 2(a + b + m(b + c))$，化简得 $a+b = (n - 2m)(b + c)$。

那么，$n$ 和 $m$ 分别是几圈呢？

当慢指针第一次进入环的起始位置时（假设为位置 $A$），由于快指针一定在慢指针前面，所以此时快指针已经在环上（假设为位置 $B$）。因为快指针的速度是慢指针的速度的 $2$ 倍，当它们在环上移动时，慢指针移动一圈会又回到环的起点位置 $A$，此时快指针移动了两圈也回到位置 $B$。

相同的时间下，快指针在走这两圈的路上一定会遇到（且为 $1$ 次）只走一圈的满指针；且因为慢指针慢，要「追上」慢指针，快指针一定会走过环一圈，使其「落后于」慢指针，然后再相遇，故 $n = 1, m = 0$。代入 $a+b = (n - 2m)(b + c)$ 有 $a = c$。

因此，我们 只需要在快慢指针相遇时，再申请一个指针，从链表头开始走（与慢指针同速度）。当慢指针和这个新申请的指针相遇时，就是环形链表入环的第一个节点。

时间复杂度：O(n)，一趟遍历，空间复杂度：O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *slow = head, *fast = head, *node = head;
    // 判断快指针能不能再往后移动两个节点
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        // 相遇
        if (slow == fast) {
            break;
        }
    }

    // 未相遇
    if ((fast == NULL) || (fast->next == NULL)) {
        return NULL;
    }
    
    // 确定环形链表入环的第一个节点
    while (node != slow) {
        node = node->next;
        slow = slow->next;
    }
    return node;
}