AHA'S BOOK

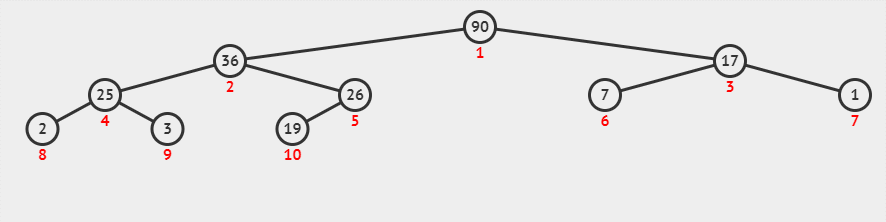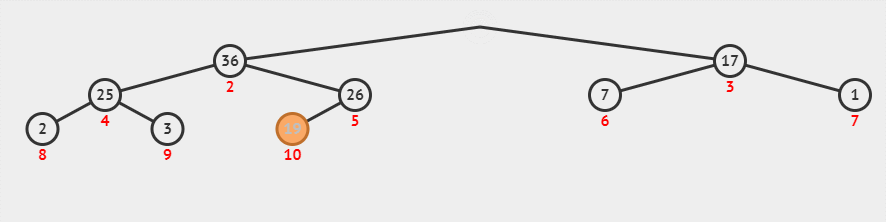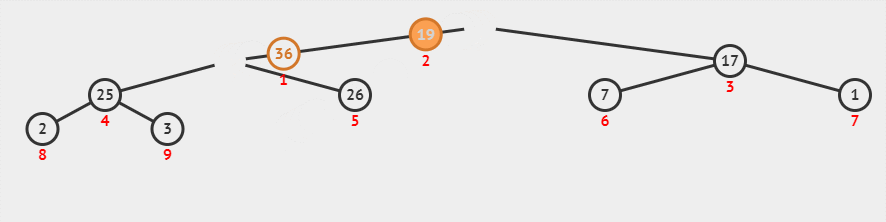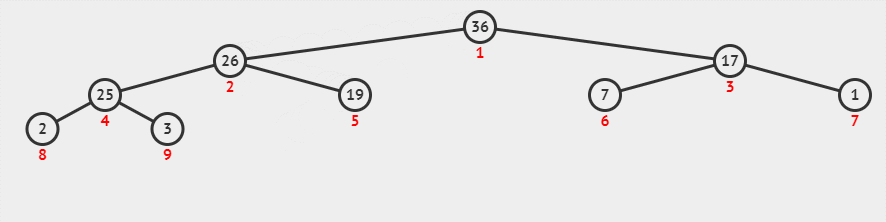
堆（Heap）是一类特殊的数据结构，是最高效的优先级队列。堆是用 数组实现 的完全 二叉树，没有使用父指针或者子指针，省内存。

完全二叉树的形式是指除了最后一层之外，其他所有层的结点都是满的，而最后一层的所有结点都靠左边。

堆属性

堆属性 ：在最大堆中，父结点的值比每一个子结点的值都要大（可以等于）。在最小堆中，父结点的值比每一个子结点的值都要小（可以等于）。这就是所谓的「堆属性」，并且这个属性对堆中的 每一个结点 都成立。

在一个最大堆中，最小元素一定在叶子结点中，但不能确定是哪一个；在一个最小堆中，最大元素一定在叶子结点中，但不能确定是哪一个。

下面是一个堆数据的二叉树模式图和紧凑数组模式图。

二叉树模式图：

堆的二叉树模式图

紧凑数组模式图：

堆的紧凑数组模式图

堆的根结点存放的是最大或者最小元素，但是 其他结点的排序顺序是未知的，只是满足堆属性而已。

堆与普通树的区别

  1. 结点顺序：在最大堆中，任一根结点都不小于其左、右子结点的值，而在二叉搜索树中，根结点一定大于其左结点的值，也一定小于其右结点的值。

  2. 内存占用：普通树占用的内存比其存储的数据要多，因为要为每个结点对象及其左、右子结点指针分配内存，而堆仅仅使用一个数组存储数据，不需要指针。

  3. 平衡：二叉搜索树时间复杂度为 O(log n) 的前提是树尽可能是平衡的。而堆中平衡不是问题，只要满足堆属性即可保证 O(log n) 的性能。

  4. 搜索 ：二叉搜索树中搜索很快，即二分查找 O(log n)。但是，在堆中搜索很慢，即遍历数组 O(n)，在堆中搜索不是第一优先级，因为 使用堆的目的是将最大（或者最小）的结点放在最前面，从而快速的进行相关插入、删除操作。

堆中父我子节点映射关系

父我子结点映射关系：对于数组中索引为 ii 的结点（我），其父结点索引和左、右子结点在数组中的索引位置为如下：

{my(i)=i;parent(i)=floor(i−12);left(i)=2i+1;right(i)=2i+2=left(i)+1;\begin{cases} my(i) = i; \\ parent(i) = floor(\frac{i-1}{2}); \\ left(i) = 2i+1; \\ right(i) = 2i + 2 = left(i) + 1; \\ \end{cases}

所有结点的索引一定不能越界，即 i∈[0,n−1]i \in [0, n-1]。

堆数组元素大小关系

数组关系：根据堆属性可知，在最大堆中有 array[parent(i)]>=array[i]array[parent(i)] >= array[i] ，在最小堆中有 array[parent(i)]<=array[i]array[parent(i)] <= array[i]。

堆的二叉树模式的高度

堆的形状一定是一棵 完全 二叉树。在堆中，在当前层级所有的结点都已经填满之前不允许开始下一层的填充。

一个有 nn 个结点的堆，其高度为 h=floor(log2n)h=floor(log_{2}{n})。堆的前 h−1h-1 层结点数量为 2h−12^{h}-1。堆的最后一层若填满的话，最后一层包含 2h2^h 个结点，整个堆共有 n=2h+1−1n=2^{h+1}-1 个结点。

叶结点总是位于数组的 [floor(n/2),n−1][floor(n/2), n-1] 区间，那么 最后一个非叶子结点（最后一个内部结点）索引即 floor(n/2)−1floor(n/2)-1。

堆的高度从 0 层开始，空堆的高度为 -1，高度为 hh 的堆有 h+1h + 1 层（0 到 h 层）。

堆化（heapify）

「堆化」的目的是在堆进行插入或删除操作后，为了确保堆仍然是一个有效的最大堆或最小堆（仍然满足堆属性），需要进行一些必要的操作（上浮和下沉操作），这个过程就叫做堆化。

  1. shiftUp(): If the element is greater (max-heap) or smaller (min-heap) than its parent, it needs to be swapped with the parent. This makes it move up the tree.
  2. shiftDown(). If the element is smaller (max-heap) or greater (min-heap) than its children, it needs to move down the tree.

上浮或下沉是一个递归过程，需要 O(log n) 时间。因为每次上浮或下沉都会选择一个子树、而抛弃另一个子树（上浮或下沉的次数最多为树的高度）。

为什么在插入或删除时，会有上浮和下沉过程？

这是因为，删除操作时，会 pop 出堆顶的元素，并将堆数组的最后一个索引的元素填充到堆顶，这个操作会使得堆不再满足堆属性；而在插入操作时，会先将数据存储在堆数组的最后一个索引后面，插入的数据大小未知，也会导致堆不再满足堆属性。因此，在插入或删除操作执行后，需要进行堆化这一过程。

数组实现堆数据结构

堆结构定义

1
2
3
4
5
typedef struct Heap {
    int *array;     // 堆的数组
    int size;       // 堆的当前大小
    int capacity;   // 堆的容量
} Heap_t;

堆结构与之前的栈的结构类似，包括堆的最大容量、堆的当前大小（数据量）、存储数据的空间（数组）。

这里，堆的数据成员使用一个指针，可以在创建不同的堆时，根据需要申请堆的容量；如果使用一个数组变量（如 int array[MAX_CAPACITY]），则在创建不同的堆时，无法修改堆的最大容量。
这里，堆的数据成员使用一个 int * 类型的指针，如果我们堆中存放的数据是复杂的组合数据，简单地修改数据成员的指针类型即可。

堆的初始化

堆的初始化，包括申请堆本身的内存空间和数据成员的内存空间两部分，以及对基本成员做初始化操作。

1
2
3
4
5
6
7
8
9
10
11
// 初始化堆
Heap_t* initHeap(int capacity) {
    if (capacity <= 0) {
        return NULL;
    }
    Heap_t *heap = (Heap_t *)malloc(sizeof(Heap_t));
    heap->array = (int *)malloc(capacity * sizeof(int));
    heap->size = 0;
    heap->capacity = capacity;
    return heap;
}

获取父节点索引

根据上述的理论基础，我们知道当前节点 ii 的父节点的索引为 parent(i)=floor(i−12)parent(i) = floor(\frac{i-1}{2})。

1
2
3
4
// 获取节点的父节点索引
int getParentIndex(int index) {
    return (index - 1) >> 1;
}

获取左子节点索引

根据上述的理论基础，我们知道当前节点 ii 的左子节点的索引为 left(i)=2i+1left(i) = 2i+1。

1
2
3
4
// 获取节点的左子节点索引
int getLeftChildIndex(int index) {
    return (index << 1) + 1;
}

获取右子节点索引

根据上述的理论基础，我们知道当前节点 ii 的右子节点的索引为 right(i)=2i+2right(i) = 2i+2。

1
2
3
4
// 获取节点的右子节点索引
int getRightChildIndex(int index) {
    return (index << 1) + 2;
}

堆化之上浮操作

在插入操作时，会先将数据存储在堆数组的最后一个索引后面，而插入的数据大小未知，会导致堆不再满足堆属性，需要进行堆化中的上浮操作，使堆数组重新满足堆属性。

首先，封装一个实现交换数组中两个位置的值的函数。这里，使用了异或运算的自反性，而没有使用临时变量的方式交换两个数。

1
2
3
4
5
void swap(int *array, int idx1, int idx2) {
    array[idx1] = array[idx1] ^ array[idx2];
    array[idx2] = array[idx1] ^ array[idx2];
    array[idx1] = array[idx1] ^ array[idx2];
}

在最大堆的堆化上浮操作中，如果当前索引对应的节点的值比其父节点的值大，则应该将两个节点进行交换，直到不满足当前节点比其父节点大或当前节点达到堆顶为止。

1
2
3
4
5
6
7
8
9
10
// 上浮操作，将节点移动到正确的位置
void siftUp(Heap_t *heap, int index) {
    int *array = heap->array;
    int parentIndex = getParentIndex(index);
    while ((index > 0) && (array[index] > array[parentIndex])) {
        swap(array, parentIndex, index);
        index = parentIndex;  // 交换节点后, 更新当前节点的位置
        parentIndex = getParentIndex(index);  // 重新获取父节点位置
    }
}

堆化之下沉操作（迭代方式）

在删除操作时，会 pop 出堆顶的元素，并将堆数组的最后一个索引的元素填充到堆顶，这个操作会使得堆不再满足堆属性，需要进行堆化中的下沉操作 —— 将这个数放到合适它的位置，使堆数组重新满足堆属性。

在最大堆的堆化下沉操作中，当前索引对应的节点的值要跟它的左右孩子节点做比较，并跟两者中较大的孩子做位置替换，直到无需跟左右孩子节点替换（值比它俩都大）为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 下沉操作，将节点移动到正确的位置
void siftDown(Heap_t *heap, int index) {
    int *array = heap->array;
    int size = heap->size;
    int leftChildIndex, rightChildIndex, maxIndex;
    while (index < size) {
        leftChildIndex = getLeftChildIndex(index);
        rightChildIndex = getRightChildIndex(index);
        
        // 接下来的两个判断为找出具有更大值的孩子的索引
        maxIndex = index;
        if (leftChildIndex < size && array[leftChildIndex] > array[maxIndex]) {
            maxIndex = leftChildIndex;
        }
        if (rightChildIndex < size && array[rightChildIndex] > array[maxIndex]) {
            maxIndex = rightChildIndex;
        }

        if (maxIndex != index) {
            swap(array, maxIndex, index);
            index = maxIndex;
        } else {
            break;
        }
    }
}

while 循环处的条件其实为 true 也行, 代码里那么写是防止首次进入 while 循环时，便是非法的索引，这样可以少一次循环处理。

堆化之下沉操作（递归方式）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void siftDown(Heap_t* heap, int index) {
    int maxIndex = index;
    int leftChildIndex = getLeftChildIndex(index);
    int rightChildIndex = getRightChildIndex(index);

    // 接下来的两个判断为找出具有更大值的孩子的索引
    if (leftChildIndex < heap->size && heap->array[leftChildIndex] > heap->array[maxIndex]) {
        maxIndex = leftChildIndex;
    }

    if (rightChildIndex < heap->size && heap->array[rightChildIndex] > heap->array[maxIndex]) {
        maxIndex = rightChildIndex;
    }

    if (index != maxIndex) {
        swap(heap->array, maxIndex, index);
        siftDown(heap, maxIndex);  // 递归方式
    }
}

获取堆顶元素

1
2
3
4
5
6
7
8
// 获取堆顶元素
int peek(Heap_t *heap) {
    if (heap->size <= 0) {
        printf("Heap is empty!\n");
        return -1;
    }
    return heap->array[0];
}

插入数据

在插入操作时，会 先将数据存储在堆数组的最后一个索引后面 ，而插入的数据大小未知，会导致堆不再满足堆属性，需要 进行堆化中的上浮操作，使堆数组重新满足堆属性。

下面的动画演示了插入 2,7,26,25,19,17,1,90,3,36 数据（创建堆并维持堆属性）的过程。
堆插入数据

1
2
3
4
5
6
7
8
9
10
// 插入元素
void push(Heap_t *heap, int value) {
    if (heap->size >= heap->capacity) {
        printf("Heap is full!\n");
        return;
    }
    heap->array[heap->size] = value;  // 存储在堆数组的最后一个索引后面
    siftUp(heap, heap->size);  // 进行堆化中的上浮操作
    heap->size++;
}

如果不希望遇到堆满的情况（希望在堆满时依然可以插入数据），则可以在堆满时进行动态扩容，并修改堆的容量。

删除堆顶数据

在删除操作时，会 pop 出堆顶的元素，并 将堆数组的最后一个索引的元素填充到堆顶 ，这个操作会使得堆不再满足堆属性，需要 进行堆化中的下沉操作 —— 将这个数放到合适它的位置，使堆数组重新满足堆属性。

下面的动画演示了删除堆顶数据的过程。
删除堆顶数据过程

1
2
3
4
5
6
7
8
9
10
11
12
// 删除堆顶元素
int pop(Heap_t *heap) {
    if (heap->size <= 0) {
        printf("Heap is empty!\n");
        return -1;
    }
    int top = heap->array[0];
    heap->array[0] = heap->array[heap->size - 1];
    heap->size--;
    siftDown(heap, 0);
    return top;
}

删除堆顶后的紧凑型数组模式图是这样的：
删除堆顶数据后

打印堆数据

1
2
3
4
5
6
7
8
// 打印堆元素
void printHeap(Heap_t *heap) {
    printf("Heap: ");
    for (int i = 0; i < heap->size; ++i) {
        printf("%d ", heap->array[i]);
    }
    printf("\n");
}

销毁堆

1
2
3
4
5
// 销毁堆
void destroyHeap(Heap_t *heap) {
    free(heap->array);
    free(heap);
}

堆操作的时间复杂度

堆的时间复杂度如下：

  • 插入元素到堆：O(log n)
  • 删除堆顶元素：O(log n)
  • 获取堆顶元素：O(1)
  • 「Floyd 上浮方式」构建堆：O(n)
  • 堆排序：O(n*log n)
  • 上浮操作：O(n*log n)
  • 下沉操作：O(n*log n)

为什么构建堆的过程的时间复杂度为 O(n) 呢？

数组实现堆完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct {
    int *array;     // 堆的数组
    int size;       // 堆的当前大小
    int capacity;   // 堆的容量
} Heap_t;

void swap(int *array, int idx1, int idx2) {
    array[idx1] = array[idx1] ^ array[idx2];
    array[idx2] = array[idx1] ^ array[idx2];
    array[idx1] = array[idx1] ^ array[idx2];
}

Heap_t* initHeap(int capacity) {
    if (capacity <= 0) {
        return NULL;
    }
    Heap_t *heap = (Heap_t *)malloc(sizeof(Heap_t));
    heap->array = (int *)malloc(capacity * sizeof(int));
    heap->size = 0;
    heap->capacity = capacity;
    return heap;
}

int getParentIndex(int index) {
    return (index - 1) >> 1;
}

int getLeftChildIndex(int index) {
    return (index << 1) + 1;
}


int getRightChildIndex(int index) {
    return (index << 1) + 2;
}

void siftUp(Heap_t *heap, int index) {
    int *array = heap->array;
    int parentIndex = getParentIndex(index);
    while ((index > 0) && (array[index] > array[parentIndex])) {
        swap(array, parentIndex, index);
        index = parentIndex;  // 交换节点后, 更新当前节点的位置
        parentIndex = getParentIndex(index);  // 重新获取父节点位置
    }
}

void siftDown(Heap_t* heap, int index) {
    int maxIndex = index;
    int leftChildIndex = getLeftChildIndex(index);
    int rightChildIndex = getRightChildIndex(index);

    // 接下来的两个判断为找出具有更大值的孩子的索引
    if (leftChildIndex < heap->size && heap->array[leftChildIndex] > heap->array[maxIndex]) {
        maxIndex = leftChildIndex;
    }

    if (rightChildIndex < heap->size && heap->array[rightChildIndex] > heap->array[maxIndex]) {
        maxIndex = rightChildIndex;
    }

    if (index != maxIndex) {
        swap(heap->array, maxIndex, index);
        siftDown(heap, maxIndex);  // 递归方式
    }
}

int peek(Heap_t *heap) {
    if (heap->size <= 0) {
        printf("Heap is empty!\n");
        return -1;
    }
    return heap->array[0];
}

void push(Heap_t *heap, int value) {
    if (heap->size >= heap->capacity) {
        printf("Heap is full!\n");
        return;
    }
    heap->array[heap->size] = value;  // 存储在堆数组的最后一个索引后面
    siftUp(heap, heap->size);  // 进行堆化中的上浮操作
    heap->size++;
}

int pop(Heap_t *heap) {
    if (heap->size <= 0) {
        printf("Heap is empty!\n");
        return -1;
    }
    int top = heap->array[0];
    heap->array[0] = heap->array[heap->size - 1];
    heap->size--;
    siftDown(heap, 0);
    return top;
}

void printHeap(Heap_t *heap) {
    printf("Heap: ");
    for (int i = 0; i < heap->size; ++i) {
        printf("%d ", heap->array[i]);
    }
    printf("\n");
}

void destroyHeap(Heap_t *heap) {
    free(heap->array);
    free(heap);
}

int main(int argc, char *argv[]) {
    int size = 10, capacity = 10;
    int nums[] = {2,7,26,25,19,17,1,90,3,36};
    Heap_t *heap = initHeap(capacity);
    for (int i = 0; i < size; ++i) {
        push(heap, nums[i]);
    }
    printHeap(heap);
    printf("Heap top: %d\n", peek(heap));
    printf("Heap pop: %d\n", pop(heap));
    printf("Heap top: %d\n", peek(heap));
    printHeap(heap);
    destroyHeap(heap);
    return 0;
}

程序的输出结果为：

1
2
3
4
5
Heap: 90 36 17 25 26 7 1 2 3 19
Heap top: 90
Heap pop: 90
Heap top: 36
Heap: 36 26 17 25 19 7 1 2 3

参考资料：

  1. Heap in swift-algorithm-club
  2. 堆的动画制作网站
aha
2023-10-18
数据结构 堆
Expand all Back to top Go to bottom Search in blogs
银河白
豆沙绿
杏仁黄
青草绿
秋叶褐