AHA'S BOOK

并查集（Union-Find Disjoint Sets, UFDS）是一种用于处理一些不相交集合的数据结构，实现为一个森林，其中的每棵树表示一个集合，树中的节点表示对应集合中的元素。

顾名思义，并查集支持两种操作：

  • 合并（Union）：合并两个元素所属集合（合并对应的树），通常是将两个集合的根节点连接在一起。
  • 查找（Find）：查找某个元素所属集合，通常是找到该元素所在集合的根节点，这可以用于判断两个元素是否属于同一集合。

下图是一个具有四个不相交集合的树构成的森林。

并查集应用场景

并查集数据结构最常见的应用是跟踪无向图的连接组件。它还用于实现 Kruskal 算法的高效版本，以查找图的最小生成树。

关于并查集的应用，后面的学习中再做整理~

并查集实现

上面介绍了什么是并查集，并给出了并查集支持的一些操作。下面开始，逐步实现基于数组的并查集。

初始化

并查集的实现可以使用数组来表示每个元素所属的集合，其中：

  • 数组的索引表示元素的值；
  • 数组的值表示该元素所属的集合的代表元素。

一般用树的根节点作为该集合的代表元素。

初始时，每个元素都是独立的集合，它属于它自己（表示为一棵只有根节点的树），即每个元素的值和索引相同（将根节点的父亲设为自己）。

初始化时，就像这样，自己指向自己，树的高度为 0。

1
2
3
4
5
6
7
// 初始化并查集
void init(int parent[], int rank[], int size) {
    for (int i = 0; i < size; ++i) {
        parent[i] = i;
        rank[i] = 0;
    }
}

这里 rank[i] 的值是以顶点 i 为根的子树高度的上限，它用作后面 UnionSet(i, j) 操作的引导启发式。先不用管 rank[i] 了，后面还会遇到。

查找

就像文章一开头说的那样，并查集的查找操作，是查找某个元素所属集合，通常是找到该元素所在集合的根节点。具体地，

  • 查找当前元素的父元素，若父元素不是自己，则更新它为当前元素，并查找它的父元素，直到当前元素的父元素是自己为止。

并查集查找（迭代实现）

朴素的并查集查找操作（迭代实现）：

1
2
3
4
5
6
7
// 查找元素所属的集合
int findSet(int parent[], int x) {
    while (parent[x] != x) {
        x = parent[x];
    }
    return x;
}

并查集查找（递归实现）

朴素的并查集查找操作（递归实现）：

1
2
3
4
5
6
7
8
// 查找元素所属的集合
int findSet(int parent[], int x) {
    if (parent[x] == x) {
        return x;
    } else {
        return findSet(parent, parent[x]);
    }
}

并查集查找（带路径压缩）

想一想，一个集合中的所有元素，虽然有共同的代表元素，但是这棵树可能呈现不同的形状。

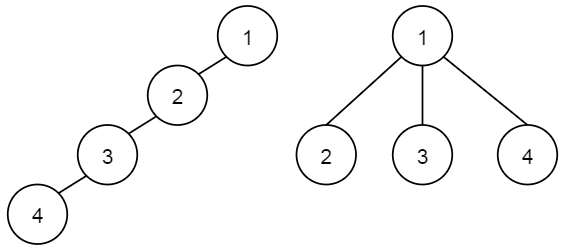
上面这张图中，左边与右边集合中的元素一致，且代表元素都是 1，但是树的形状不同。这样的话，对于同一个元素（比如 4），查找到其代表元素 1 的迭代（递归）次数是不一样的，左边需要 3 次才能完成，而右边只需要 1 次就能完成。

因此，为了提高效率，就需要尽可能降低迭代（递归）次数。这就需要进行「路径压缩」。

想一想，上面递归方式实现的查找操作 findSet(int parent[], int x) 中，是查找元素 x 的代表元素并返回。在这个函数内部，如果当前元素的父元素不是代表元素，函数会递归的查找其父元素的代表元素（我们被划分在同一个集合中了，假如我的代表元素是 R，那么我的父元素的代表元素也是 R 呀）。

因此，我们可以 在递归的过程中，更新当前元素的代表元素，从而实现「路径压缩」，以加快后续查找。

并查集查找操作（带路径压缩的递归实现）：

1
2
3
4
5
6
7
8
9
10
11
// 查找元素所属的集合
int findSet(int parent[], int x) {
    if (parent[x] == x) {
        return x;
    } else {
        // 路径压缩，findSet() 返回的就是参数 2 的最终代表元素，
        // 所以，在递归过程中传入的不同参数 2 的最终代表元素都是 findSet() 的返回值
        parent[x] = findSet(parent, parent[x]);
        return parent[x];
    }
}

并查集查找操作（带路径压缩的迭代实现）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 查找元素所属的集合
int findSet(int parent[], int x) {
    int rootOfx = x;  // 初始时，暂定 x 的代表元素是自己

    // 寻找 x 的代表元素，存储在 rootOfx 中
    while (parent[rootOfx] != rootOfx) {
        rootOfx = parent[rootOfx];
    }

    // 现在 rootOfx 已经是 x 真正的代表元素了

    // 迭代地进行路径压缩
    while (parent[x] != x) {
        x = parent[x];
        // 逐级更新路径上的节点，它们有共同的最终代表元素 rootOfx
        parent[x] = rootOfx;
    }

    return rootOfx;
}

路径压缩查找示例

假如，我们有如下的不相交集合：

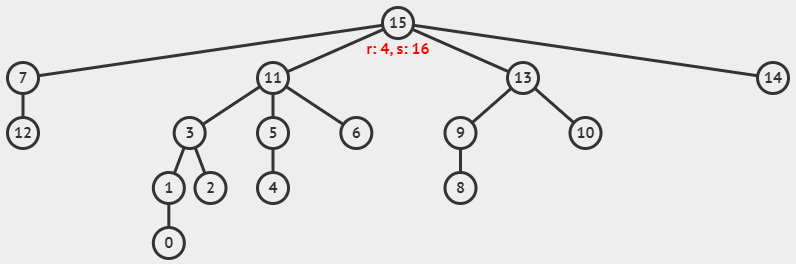
现在，我们使用带路径压缩的并查集查找函数，查找元素 1 的代表元素，这一过程可以可视化为下面的动画。

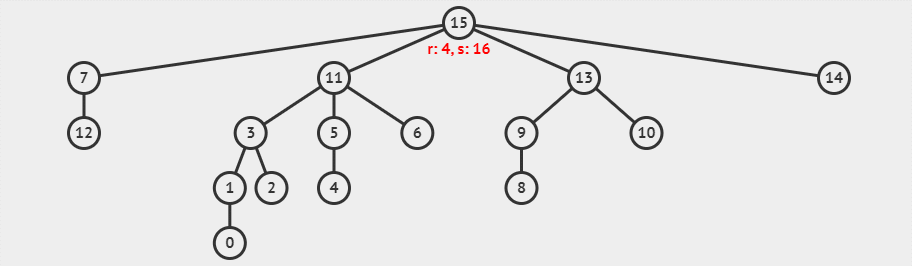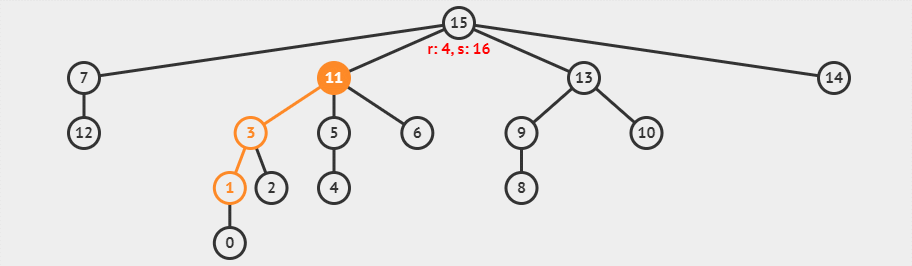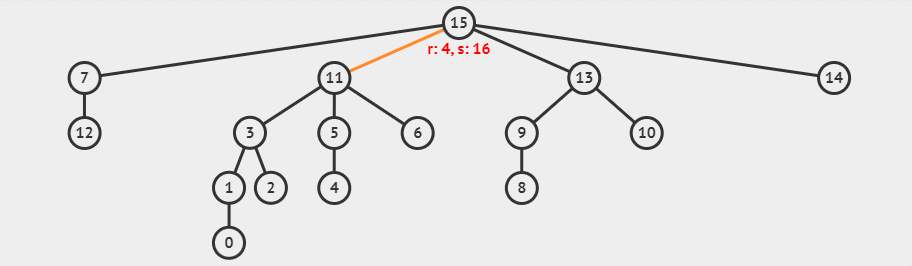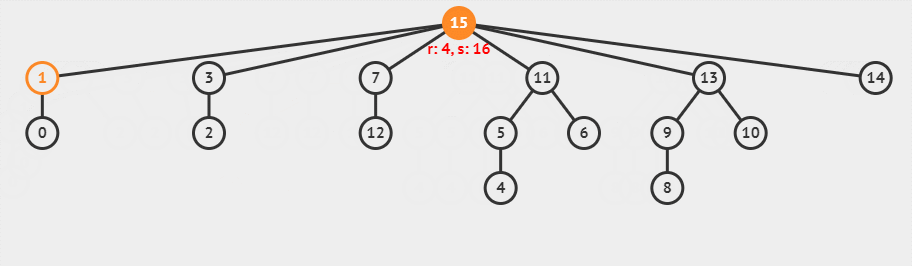
图中 r 就是 rank 的缩写，s 代表的是元素的数量。

合并

要合并两棵树（集合），我们只需要将一棵树的根节点连到另一棵树的根节点。要完成这一操作，我们需要：

  1. 查找一个元素 x 的代表元素；
  2. 查找另一个元素 y 的代表元素；
  3. 若两者的代表元素不同，则将其中一棵树的根节点连接到另一棵树的根节点上；若两者的代表元素相同，则无需合并。
1
2
3
4
5
6
7
8
9
10
// 合并两个集合
void unionSet(int parent[], int x, int y) {
    int rootX = findSet(parent, x);
    int rootY = findSet(parent, y);
    // 属于不同集合
    if (rootX != rootY) {
        // 将前者所在的树的根节点连接到后者所在的树的根节点上
        parent[rootX] = rootY;
    }
}

启发式合并

合并时，选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。我们可以 将节点较少或深度（树高）较小的树连接到另一棵，以免发生退化。

这样做的目的是尽量避免将较大的树作为子树合并到较小的树上，从而保持树的平衡，减小树的高度。

在并查集中，「退化」指的是树结构变得非常不平衡，即树的高度非常大，接近于线性结构（如链表）。

因此，在初始化小节中，数组 rank[i] 就是用来维护以顶点 i 为根的子树高度的上限，它就是在这里被使用的啦。

启发式合并（以树高为标准）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void unionSet(int parent[], int rank[], int x, int y) {
    int rootX = findSet(parent, x);
    int rootY = findSet(parent, y);
    // 属于不同集合
    if (rootX != rootY) {
        // 将深度较小的树连到另一棵树
        if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;
        } else if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX;
        } else {
            // 将前者所在的树的根节点连接到后者所在的树的根节点上
            // 被连接的树的高度将会加一, 对应的 rank 值加一
            parent[rootX] = rootY;
            rank[rootY]++;
        }
    }
}

在初始化时，每个元素都是一个独立的集合，每个树的高度都为 0：

  • 在进行第一次集合合并时（比如元素 1 和元素 3），则 unionSet(parent, rank, 1, 3) 操作，会合并为一棵 3->1 的树，其中 3 为根节点，这棵新树会长高一个单位；
  • 在进行第二次集合合并时（比如元素 1 和元素 4），则 unionSet(parent, rank, 1, 4) 操作，会合并为一棵 4<-3->1 的树，其中 3 为根节点，由于 1 所在的树高大于 4 所在的树高，因此在合并后，树高不会变得更高，因此不会更新 rank 值。

注意：在启发式合并的过程中，只能保证根节点对应 rank 值是正确的，不能保证其它位置的 rank 值的正确性。

启发式合并示例

假如，我们有如下几个不相交集合：

现在，我们使用以树高为标准的启发式合并，执行 unionSet(parent, rank, 10, 8)，这一过程可以可视化为下面的动画。

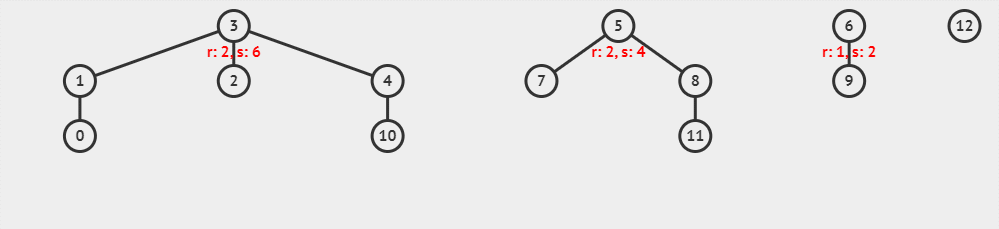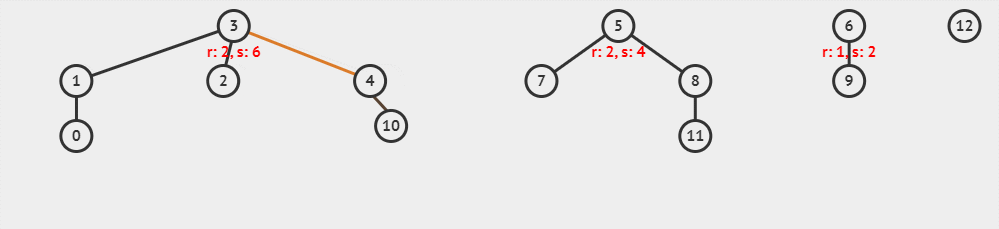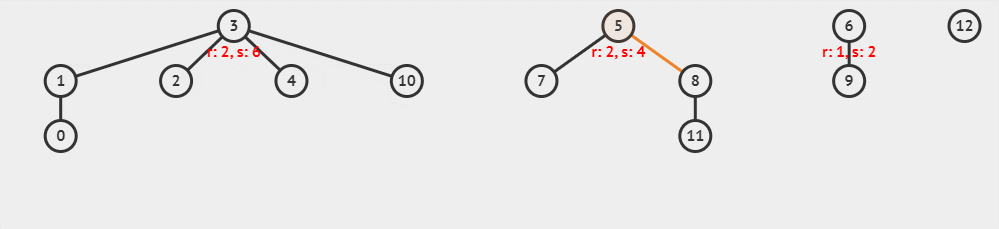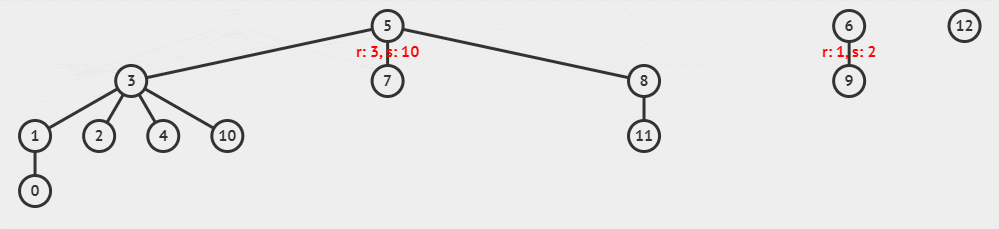
这里 x = 10, y = 8 与 x = 8, y = 10 执行后，得到的树是不一样的哦。

你可能已经发现了：在执行合并的过程中，树也会被路径压缩，这是因为并查集的合并接口调用了查找接口。

相同集合

判断两个元素是否属于同一集合。

1
2
3
int isSameSet(int parent[], int x, int y) {
    return findSet(parent, x) == findSet(parent, y);
}

并查集复杂度

时间复杂度：

  • 初始化：O(n)
  • 朴素查找：O(n)
  • 带路径压缩的查找：O(h)，可以优化至 O(α(n))，其中 h 是树的高度，足够平衡时 h = log(n)，α 是阿克曼函数
  • 带路径压缩的合并：O(h)，可以优化至 O(α(n))

空间复杂度：O(n)

这里的并查集数据结构的实现，是采用的 Quick Union 方式，而不是 Quick Find 方式。

并查集完整代码测试

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void init(int parent[], int rank[], int size) {
    for (int i = 0; i < size; ++i) {
        parent[i] = i;
        rank[i] = 0;
    }
}

int findSet(int parent[], int x) {
    if (parent[x] == x) {
        return x;
    } else {
        // 路径压缩
        parent[x] = findSet(parent, parent[x]);
        return parent[x];
    }
}

void unionSet(int parent[], int rank[], int x, int y) {
    int rootX = findSet(parent, x);
    int rootY = findSet(parent, y);
    // 属于不同集合
    if (rootX != rootY) {
        // 将深度较小的树连到另一棵树
        if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;
        } else if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX;
        } else {
            // 将前者所在的树的根节点连接到后者所在的树的根节点上
            // 被连接的树的高度将会加一, 对应的 rank 值加一
            parent[rootX] = rootY;
            rank[rootY]++;
        }
    }
}

int isSameSet(int parent[], int x, int y) {
    return findSet(parent, x) == findSet(parent, y);
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>

#define MAX_SIZE (101)

void init(int parent[], int rank[], int size);
int findSet(int parent[], int x);
void unionSet(int parent[], int rank[], int x, int y);
int isSameSet(int parent[], int x, int y);

int main() {
    int parent[MAX_SIZE];
    int rank[MAX_SIZE];
    int size = 10; // 假设有 10 个元素，从 0 到 9 编号

    init(parent, rank, size);

    // 测试 findSet 函数
    printf("findSet(0): %d\n", findSet(parent, 0));
    printf("findSet(1): %d\n", findSet(parent, 1));
    printf("findSet(2): %d\n", findSet(parent, 2));

    // 测试 unionSet 函数
    unionSet(parent, rank, 0, 1);
    unionSet(parent, rank, 2, 3);
    unionSet(parent, rank, 4, 5);
    unionSet(parent, rank, 6, 7);
    unionSet(parent, rank, 8, 9);

    printf("findSet(0): %d\n", findSet(parent, 0));
    printf("findSet(1): %d\n", findSet(parent, 1));
    printf("findSet(2): %d\n", findSet(parent, 2));
    printf("findSet(3): %d\n", findSet(parent, 3));
    printf("findSet(4): %d\n", findSet(parent, 4));
    printf("findSet(5): %d\n", findSet(parent, 5));
    printf("findSet(6): %d\n", findSet(parent, 6));
    printf("findSet(7): %d\n", findSet(parent, 7));
    printf("findSet(8): %d\n", findSet(parent, 8));
    printf("findSet(9): %d\n", findSet(parent, 9));

    unionSet(parent, rank, 6, 8);
    printf("findSet(6): %d\n", findSet(parent, 6));
    printf("findSet(8): %d\n", findSet(parent, 8));

    // 测试 isSameSet 函数
    printf("isSameSet(0, 1): %d\n", isSameSet(parent, 0, 1));
    printf("isSameSet(2, 3): %d\n", isSameSet(parent, 2, 3));
    printf("isSameSet(1, 3): %d\n", isSameSet(parent, 1, 3));
    printf("isSameSet(6, 9): %d\n", isSameSet(parent, 6, 9));

    return 0;
}

测试结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
findSet(0): 0
findSet(1): 1
findSet(2): 2
findSet(0): 1
findSet(1): 1
findSet(2): 3
findSet(3): 3
findSet(4): 5
findSet(5): 5
findSet(6): 7
findSet(7): 7
findSet(8): 9
findSet(9): 9
findSet(6): 9
findSet(8): 9
isSameSet(0, 1): 1
isSameSet(2, 3): 1
isSameSet(1, 3): 0
isSameSet(6, 9): 1

参考资料：

  1. https://visualgo.net/en/ufds
  2. https://oi-wiki.org/ds/dsu
aha
2023-10-23
数据结构 并查集
Expand all Back to top Go to bottom Search in blogs
银河白
豆沙绿
杏仁黄
青草绿
秋叶褐