LeetCode 刷题

戴克斯特拉算法（Dijkstra’s algorithm），又称迪杰斯特拉算法、Dijkstra 算法，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在 1956 年发现的算法。戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的 单源 最短路径问题。它可以应用于有向图和无向图，常被应用于网络路由、交通规划等领域。但对于带有负权边的图，Dijkstra 算法无法正确计算最短路径，需要使用其他算法，如 Bellman-Ford 算法。

Dijkstra 基本思想

Dijkstra 算法可以计算从图中的一个节点出发到其他所有节点的最短路径。它的基本思想是从源节点开始，通过选择当前距离源节点最近的未访问节点，不断更新和调整节点的最短路径和距离值，直到找到所有节点的最短路径为止。

Dijkstra 算法属于贪心策略（算法执行完后，才能得到全局最优解）。

Dijkstra 具体步骤

Dijkstra 步骤描述

Dijkstra 算法的具体步骤如下：

1. 创建一个距离数组dist[]，用于存储源节点到各个节点的最短路径长度。初始时，将源节点的距离设为 0，与源节点直接相连的节点的距离设为边的权重，其他节点的距离设为无穷大。
2. 创建一个标记数组visited[]，用于标记是否已经访问过该节点。初始时，将源节点标记为已访问，其他节点标记为未访问。
3. 以源节点为基准，遍历所有与其相邻的、未访问过的节点，计算「源节点」到这些相邻节点的距离，并从未访问的节点中选择距离「源节点」最近的节点，作为基准节点。
4. 以这个基准节点为中间节点，更新从源节点经过中间节点到达其它节点的距离到 dist[] 数组中，并将这个基准节点标记为已访问。
   • 更新的方式是：如果「从新的中间节点」到「该节点」的距离小于原本到它的距离，则更新它的值（你要从这个节点走才更近哦），并将这个中间节点作为它的前驱节点。
5. 重复步骤 3 和步骤 4，直到所有节点都被访问过。
6. 最终，dist[]数组中存储的就是源节点到其他所有节点的最短路径长度。

步骤三中的「相邻」节点包括直接与源节点相邻、通过已访问的节点间接与源节点相邻这两大类。换句话说，也就是 dist[] 数组中只要不是无穷大，就与源节点直接或间接相邻。

Dijkstra 复杂度

Dijkstra 算法的时间复杂度为 $O(|V|^{2})$，空间复杂度为$O(|V|^{2})$，主要为二维邻接矩阵、一维的距离矩阵、访问矩阵、前驱矩阵，其中 $V$ 是点集。

Dijkstra 算法图解

假设有下面这个图：

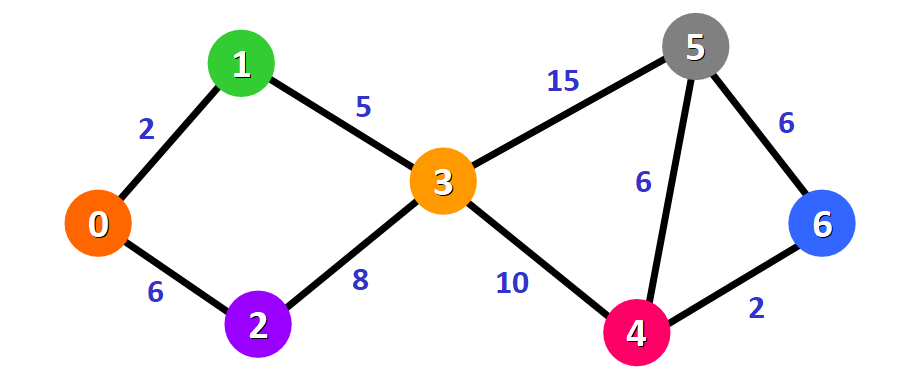
Dijkstra 算法将会寻找出图中节点 0 到所有其他节点的最短路径。

初始化 dist 数组

创建一个距离数组dist[]，用于存储源节点到各个节点的最短路径长度。初始时，源节点到自己的距离为 0，与源节点直接相连的节点的距离设为边的权重，到其它节点的距离还没有确定，所以先标记为无穷大。

1
2

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, ∞, ∞, ∞, ∞]

初始化 visited 数组

创建一个标记数组visited[]，用于标记是否已经访问过该节点。初始时，将源节点标记为已访问，其他节点标记为未访问。

1
2
3

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, ∞, ∞, ∞, ∞]
visted: [1, 0, 0, 0, 0, 0, 0]

初始化 prev 数组

创建一个前驱数组prev[]，用于存储到达该节点的最短路径上的倒数第二个节点（通过哪个节点到达的该节点）。初始时，与源节点直接相连的节点的前驱节点就是源节点，其它节点的前驱节点无法确定，先标记为无效节点（源节点到源节点的路径，没有倒数第二个节点，也标记为无效节点）。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, ∞, ∞, ∞, ∞]
visted: [1, 0, 0, 0, 0, 0, 0]
prev:  [-1, 0, 0,-1,-1,-1,-1]

记住，当所有节点都被标记为已访问（被添加到路径中）时，算法的计算过程就完成了。

遍历相邻节点

我们选择了从节点 0 出发，可以直接将它标记为「已访问」，并在图中给它加上红色的边框：

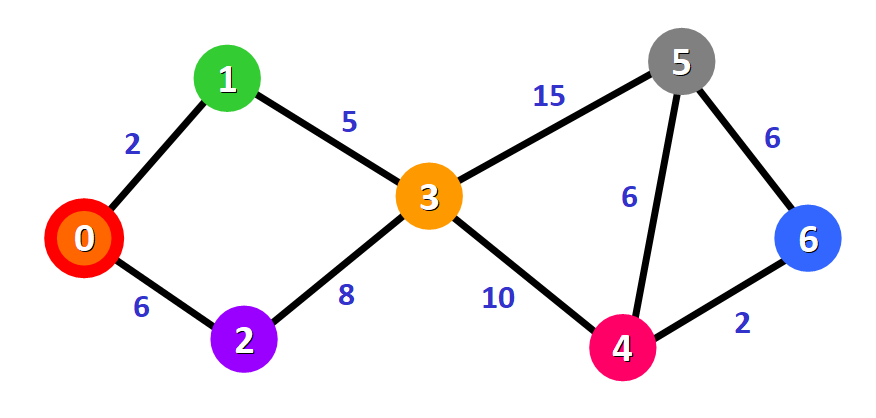
以源节点 0 为基准，遍历所有与其相邻的、未访问过的节点（节点 1 和 2），计算源节点到这些相邻节点的距离，并更新 dist[] 数组中的值。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, ∞, ∞, ∞, ∞]
visted: [1, 0, 0, 0, 0, 0, 0]
prev:  [-1, 0, 0,-1,-1,-1,-1]

从表格中可以看出，当前：

• 从源节点 0 到节点 1 的最短距离为 2（通过源节点 0 到达节点 1）；
• 从源节点 0 到节点 2 的最短距离为 6（通过源节点 0 到达节点 2）。

然后，我们 从未访问的节点（节点 1 和节点 2）中选择距离源节点最近的节点（节点 1），作为下一个基准节点，并将其标记为已访问。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, ∞, ∞, ∞, ∞]
visted: [1, 1, 0, 0, 0, 0, 0]
prev:  [-1, 0, 0,-1,-1,-1,-1]

因此，节点 1 标记为已访问（节点 2 不标记为已访问），并更新节点 1 的上一个节点为节点 0。

图中给已访问的节点 1 加上红色的边框，上一个节点 0 到该节点 1 的路径（边）被染红：

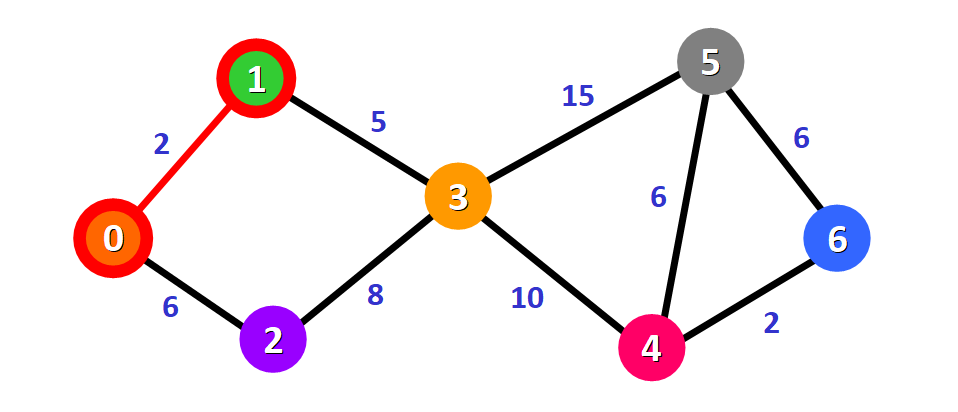
然后，节点 1 将作为下一个基准节点，重复上述遍历相邻节点的操作。

以节点 1 为基准，遍历所有与其相邻的、未访问过的节点（节点 3），计算源节点到这些相邻节点的距离，并更新 dist[] 数组中的值。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, 7, ∞, ∞, ∞]
visted: [1, 1, 0, 0, 0, 0, 0]
prev:  [-1, 0, 0,-1,-1,-1,-1]

从表格中可以看出，当前：

• 从源节点 0 到节点 3 的最短距离为 7（通过中间节点 1 到达节点 3）。
• 从源节点 0 到节点 2 的最短距离为 6（通过源节点 0 到达节点 2）。

注意，往轮遍历中未被标记为已访问的节点（这里是节点 2）也需要参与距离比较、也可作为下一个基准节点哦！

然后，我们 从未访问的节点（节点 2 和节点 3）中选择距离源节点 0 最近的节点（节点 2），作为下一个基准节点，并将其标记为已访问。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, 7, ∞, ∞, ∞]
visted: [1, 1, 1, 0, 0, 0, 0]
prev:  [-1, 0, 0,-1,-1,-1,-1]

因此，节点 2 标记为已访问（节点 3 不标记为已访问），并更新节点 2 的上一个节点为节点 0。

图中给已访问的节点 2 加上红色的边框，上一个节点 0 到该节点 2 的路径（边）被染红：

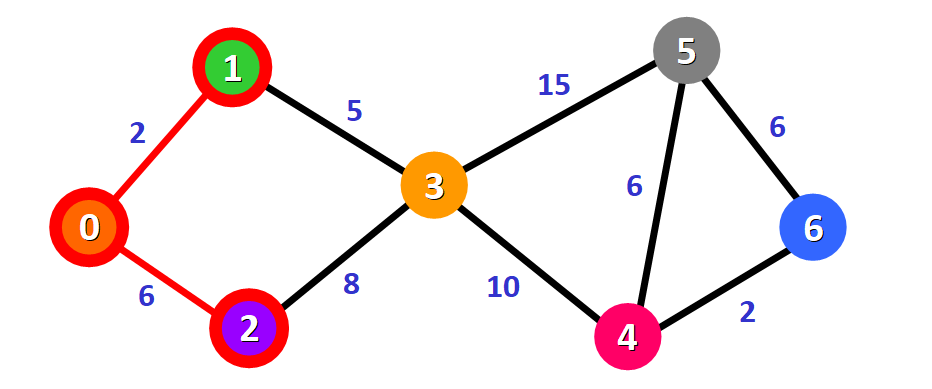
然后，节点 2 将作为下一个基准节点，重复上述遍历相邻节点的操作。

以节点 2 为基准，遍历所有与其相邻的、未访问过的节点（节点 3），计算源节点到这些相邻节点的距离，并更新 dist[] 数组中的值。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, 7, ∞, ∞, ∞]
visted: [1, 1, 1, 0, 0, 0, 0]
prev:  [-1, 0, 0,-1,-1,-1,-1]

从表格中可以看出，当前：

• 从源节点 0 到节点 3 的最短距离为 14（通过中间节点 2 到达节点 3）。
• 从源节点 0 到节点 3 的最短距离为 7（通过另一个中间节点 1 到达节点 3）。

然后，我们 从未访问的节点（节点 3）中选择距离源节点 0 最近的节点（节点 3），作为下一个基准节点，并将其标记为已访问。

1
2
3
4

node:   [0, 1, 2, 3, 4, 5, 6]
dist:   [0, 2, 6, 7, ∞, ∞, ∞]
visted: [1, 1, 1, 1, 0, 0, 0]
prev:  [-1, 0, 0, 1,-1,-1,-1]

因此，节点 3 标记为已访问，并更新节点 3 的 上一个节点为节点 1（而不是节点 2）。

图中给已访问的节点 3 加上红色的边框，上一个节点 1 到该节点 3 的路径（边）被染红：

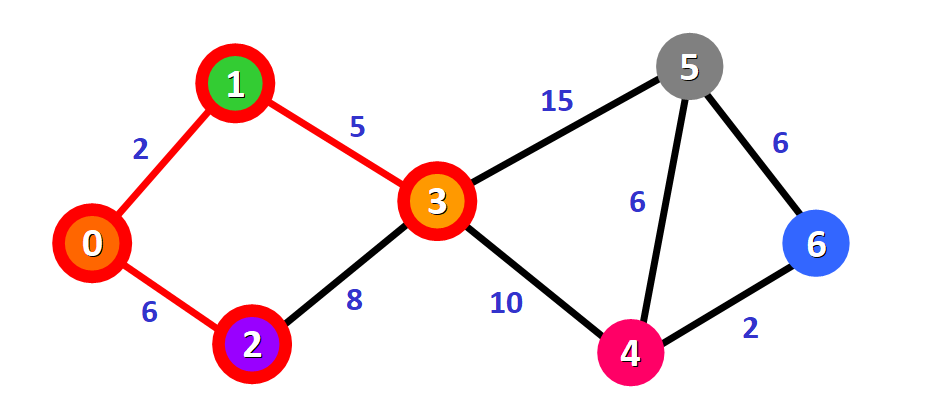
然后，节点 3 将作为下一个基准节点，重复上述遍历相邻节点的操作。

经过多次选择新的基准节点，并进行遍历相邻节点的操作后，所有节点都被标记为已访问（被添加到路径中），算法的计算过程就完成了。现在，dist[]数组中存储的就是源节点到其他所有节点的最短路径长度。

最终的表格为：

1
2
3
4

node:   [0,  1,  2,  3,  4,  5,  6]
dist:   [0,  2,  6,  7, 17, 22, 19]
visted: [1,  1,  1,  1,  1,  1,  1]
prev:  [-1,  0,  0,  1,  3,  3,  4]

最终表格对应的可视化图：

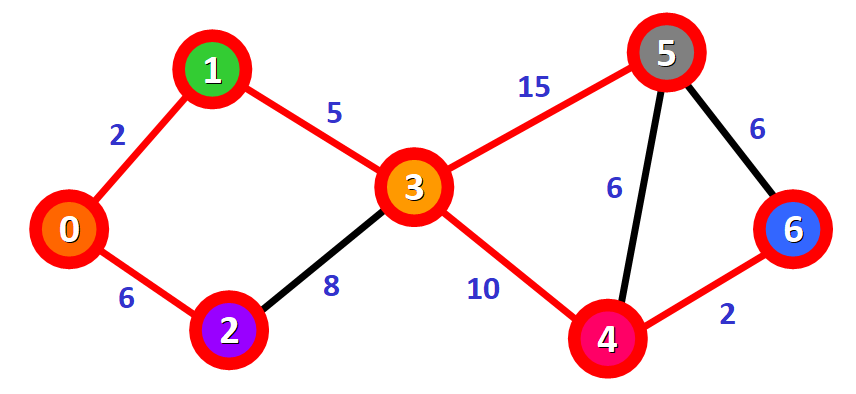
从表格或图中可以看出：

• 源节点 0 到节点 1, 2, 3, 4, 5, 6 的最短距离分别为 2, 6, 7, 17, 22, 19；
• 源节点 0 到节点 6 的最短路径为 0->1->3->4->6，这可以通过表格中的 prev[] 数组得出最短路径：节点 6 的上一个节点为 4，节点 4 的上一个节点为 3，节点 3 的上一个节点为 1，节点 1 的上一个节点为 0。

最后，再回顾一下本文开头的《具体步骤》吧~

参考资料 & 图源：

1. https://www.freecodecamp.org/chinese/news/dijkstras-shortest-path-algorithm-visual-introduction/
2. https://b23.tv/XWF7K0p