LeetCode 刷题

Floyd-Warshall 算法，中文亦称弗洛伊德算法或佛洛依德算法，是一种利用动态规划的思想解决多源（任意两点间）最短路径的算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。 Floyd-Warshall 算法的时间复杂度为 $O(|V|^{3})$，空间复杂度为 $O(|V|^{2})$，其中 $V$ 是点集（来自维基百科的定义）。

1. 「负权」指的是图中存在具有负权值的边，负权边表示从一个顶点到另一个顶点的距离是负值。Floyd-Warshall 算法可以正确处理包含负权边的图的最短路径问题。
2. 「闭包」是指图中的传递关系。在有向图中，如果存在一条路径从顶点 A 到顶点 B，那么就说顶点 A 可以到达顶点 B。传递闭包就是将所有可以通过路径到达的顶点对进行标记，形成一个闭包集合。Floyd-Warshall 算法可以用来计算有向图的传递闭包，即找出所有顶点对之间是否存在路径。
3. 「多源」指的是任意两点间的最短距离均可求出，「单源」指的是只能求一个顶点到其他点的最短距离，而不能求任意两点的最短距离。

Floyd 基本思想

Floyd 算法的基本思想是通过 中转节点来逐步优化路径长度 。该算法维护一个二维矩阵D，其中D[i][j] 表示节点 i 到节点 j 的最短路径长度。算法的核心是通过遍历所有节点 k，将节点k 作为中转节点，更新矩阵 D 的值。

Floyd 具体步骤

Floyd 步骤描述

Floyd 算法的具体步骤如下：

1. 初始化矩阵 D，使得D[i][j] 表示节点 i 到节点 j 的直接距离，如果 i 和j之间没有直接边相连，则 D[i][j] 为无穷大，如果 i 和j相同，则 D[i][j] 为0，否则为直接相连的边的权值。
2. 对于每个节点 k，遍历所有的节点i 和节点 j，如果D[i][k] + D[k][j] 的值小于 D[i][j]，则更新D[i][j] 为D[i][k] + D[k][j]。
3. 重复步骤 2，直到遍历完所有节点k。
4. 最终得到的矩阵 D 即为所有节点对之间的最短路径长度。

步骤二利用的是动态规划的思想，其状态转移方程为：D[i][j] = min(D[i][j], D[i][k] + D[k][j])；步骤一中则给出了如何初始化矩阵 D 和D[i][j]的定义。

Floyd 复杂度

Floyd 算法的时间复杂度为 $O(|V|^{3})$，空间复杂度为 $O(|V|^{2})$，其中 $V$ 是点集。它的优点是可以处理带有负权边的图，并且可以同时求解任意两个节点之间的最短路径。然而，由于其时间复杂度较高，当节点数量较大时，可能会导致算法的运行时间较长。

Floyd 算法图解

初始化距离矩阵

D[i][j]表示节点 i 到节点 j 的直接距离。初始化时，如果 i 和j之间没有直接边相连，则 D[i][j] 为无穷大，如果 i 和j相同，则 D[i][j] 为0，否则为直接相连的边的权值。

例如，节点 A 和节点 B 直接相连，权值为 2，节点 B 和节点 C 没有直接相连，权值为无穷大。

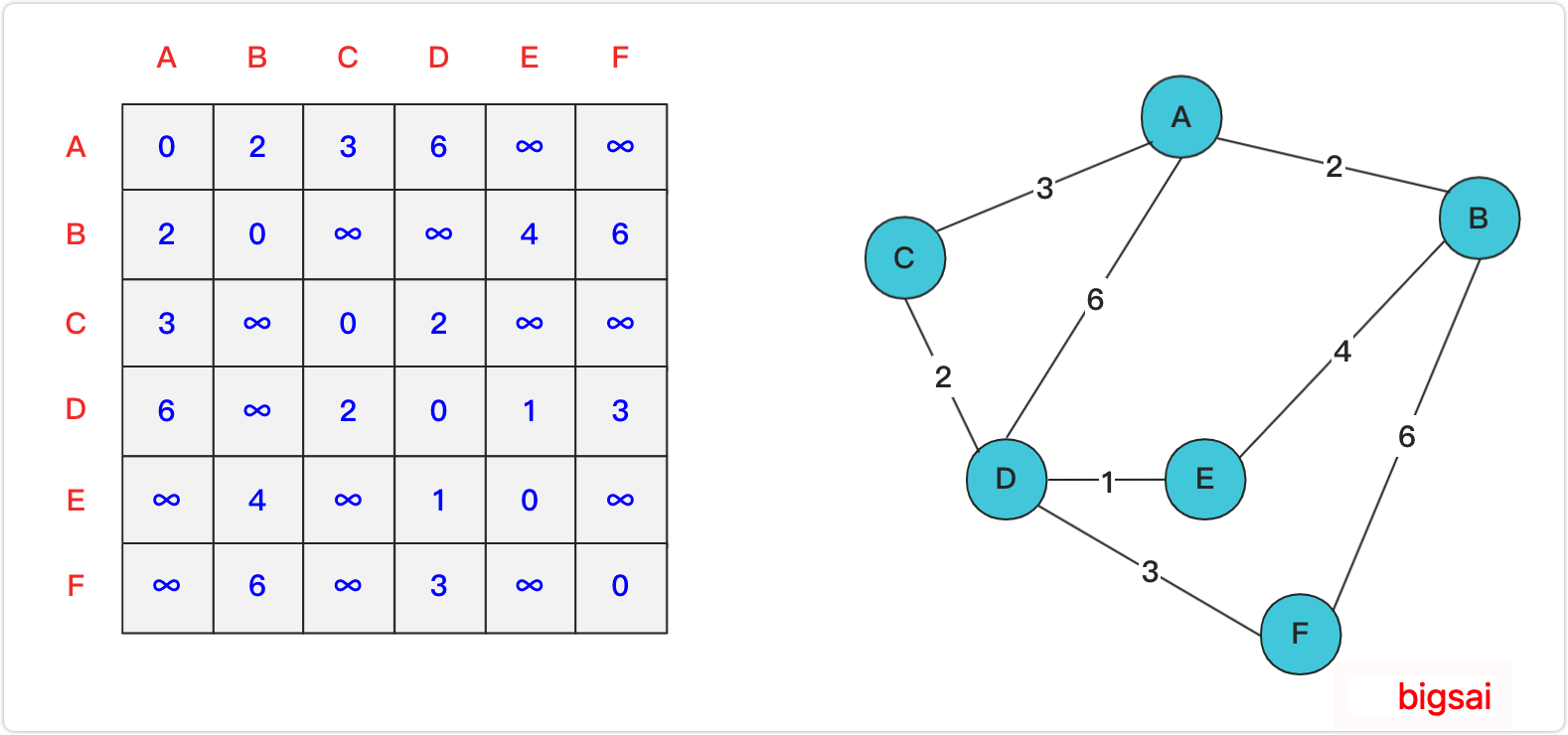
更新距离矩阵

对于每个节点 k，遍历所有的节点i 和节点 j，如果D[i][k] + D[k][j] 的值小于 D[i][j]，则更新D[i][j] 为D[i][k] + D[k][j]。

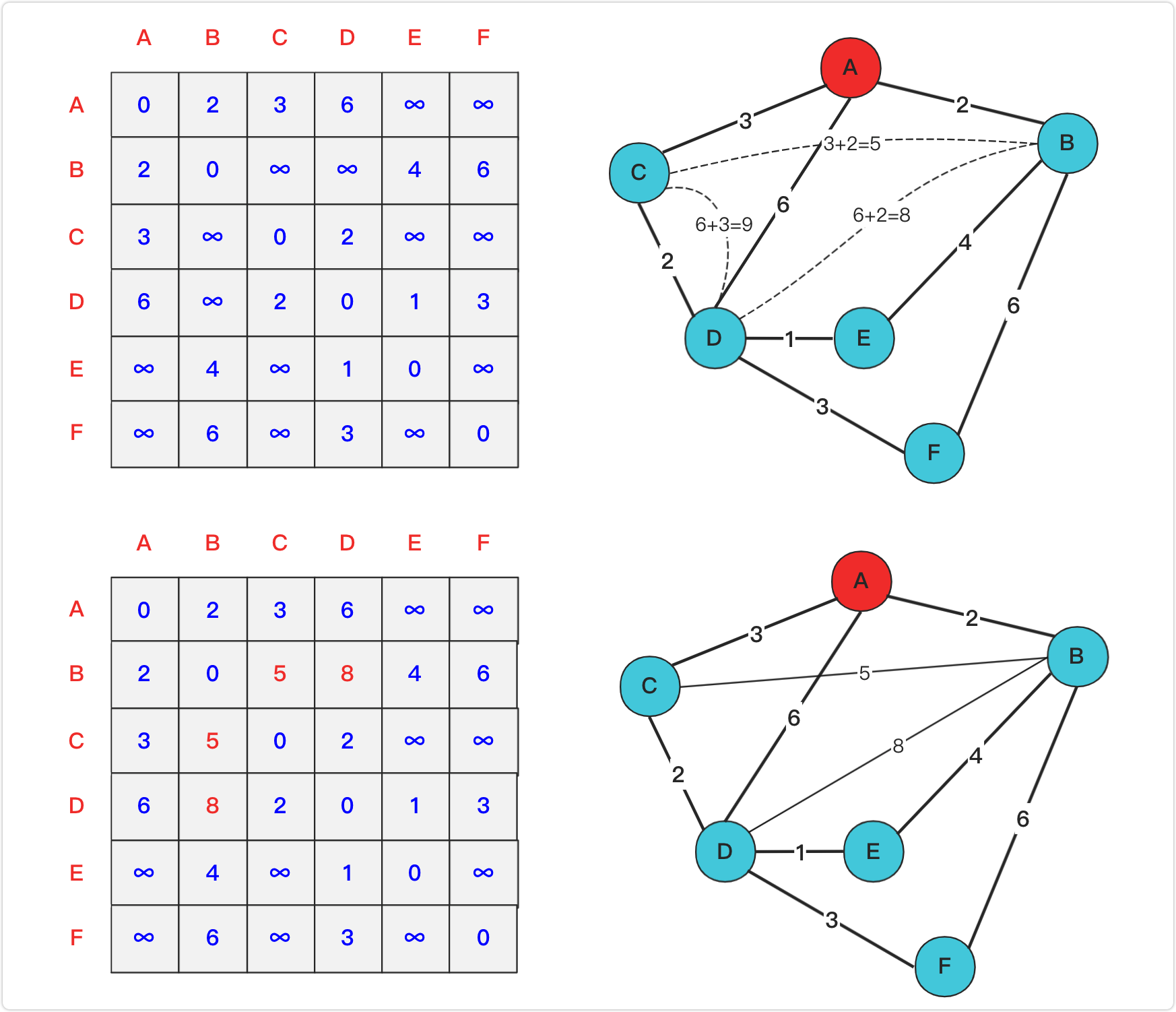
例如，当遍历节点 A 时：

• A 和 B 直接相连、A 和 C 直接相连、B 和 C 没有直接相连，因此可以通过中转节点 A 更新节点 B 和节点 C 的距离为 2+3=5。
• A 和 C 直接相连、A 和 D 直接相连、C 和 D 也直接相连，因此也可以通过中转节点 A 更新节点 C 和节点 D 的距离，但是更新的值不小于 C 和 D 直接相连的值，所有不进行更新。

Floyd 算法实现

Floyd 算法编码

假设任意两点的间的距离，存储在邻接矩阵 graph 中，如果两点之间不直接相连，则该位置的值为无穷大 inf，否则为相应的距离值。

当然，也可以通过数组直接存储直接相连的边的信息，如 [[nodeA, nodeB, distAB], ..., [nodeC, nodeZ, distCZ]]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

#include <stdio.h>
#include <limits.h>

#define inf (INT_MAX)
#define n (4)

void floydWarshall(int graph[n][n]) {
    int dist[n][n];
    int i, j, k;

    // 步骤一：初始化结果矩阵，使其等于输入图的邻接矩阵 
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            dist[i][j] = graph[i][j];
        }
    }

    // 步骤二 & 三：对每个节点 k 进行遍历，作为中转节点
    for (k = 0; k < n; k++) {
        // 遍历所有节点对(i, j)
        for (i = 0; i < n; i++) {
            for (j = 0; j < n; j++) {
                // 加入这个判断，防止后面的加法运算溢出
                if (dist[i][k] == inf || dist[k][j] == inf) {
                    continue;
                }
                // 如果通过节点 k 可以缩短路径长度，则更新 dist[i][j] 的值
                if (dist[i][k] + dist[k][j] < dist[i][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }

    // 步骤四：打印最短路径矩阵
    printf(" 最短路径矩阵为：\n");
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            if (dist[i][j] == inf) {
                printf("inf ");
            } else {
                printf("%d ", dist[i][j]);
            }
        }
        printf("\n");
    }
}

int main(int argc, char *argv[]) {
    int graph[n][n] = {{0, 5, inf, 10},
                       {inf, 0, 3, inf},
                       {inf, inf, 0, 1},
                       {inf, inf, inf, 0}};
    
    floydWarshall(graph);

    return 0;
}

该代码实现了 Floyd 算法，最终输出的结果是最短路径矩阵，显示了所有节点对之间的最短路径长度。

注意处理 inf + inf 和 x + inf 相加会造成的数据溢出。

程序运行结果

无向图 graph 中直接相连的节点：

1
2
3
4
5

[0]---5---[1]
 |         |
 10        3
 |         |
[3]---1---[2]

运行结果：

1
2
3
4
5

最短路径矩阵为：
0 5 8 9
inf 0 3 4
inf inf 0 1
inf inf inf 0

Floyd 算法优化

对于无向图，节点对 (i, j) 和节点对 (j, i)具有相同的权值（距离）。当遍历每一个中转节点时，D[i][j]的值的更新，只跟三个位置有关，即 i, j, k；而此时 k 固定，在 i, j 的双重循环下，会产生重复操作，因此我们可以只遍历矩阵右上三角部分即可，即 j 从 i + 1 开始遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13

for (k = 0; k < n; k++) {
    for (i = 0; i < n; i++) {
        for (j = i + 1; j < n; j++) {  // 去掉重复的计算 
            if (dist[i][k] == inf || dist[k][j] == inf) {
                continue;
            }
            if (dist[i][k] + dist[k][j] < dist[i][j]) {
                dist[i][j] = dist[i][k] + dist[k][j];
                dist[j][i] = dist[i][j];  // 一并更新反向节点(j, i) 的距离
            }
        }
    }
}

Floyd 算法，俗称插点法，不就一个点 k 一个点 k' 地插进去，作为中转节点，更新节点对之间的距离嘛！

参考资料 & 图源：https://www.cnblogs.com/bigsai/p/15213511.html