AHA'S BOOK

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，在表的后端（rear）进行插入操作。与堆栈一样，队列也是一种操作受限制的线性表，进行插入操作的端称为队尾，进行删除操作的端称为队头。数据的入队和出队遵循先进先出（FIFO, First-In First-Out）的原则。

这篇文章主要介绍通过链表实现队列，但会首先介绍一下队列的几种实现方式和各自的特点、适用场景。

队列的实现方式

在 C 语言中，FIFO 队列的实现方式有以下几种：

  1. 数组实现：使用一个固定大小的数组作为队列的存储空间，使用两个指针 front 和 rear 分别指向队列的头部和尾部，通过不断移动指针和调整数组元素的位置来实现入队和出队操作。

  2. 链表实现：使用链表作为队列的存储结构，通过定义一个链表节点结构体来存储队列元素的值和指向下一个节点的指针。通过调整链表节点的指针关系来实现入队和出队操作。

  3. 循环队列实现：使用一个固定大小的数组作为队列的存储空间，同时使用两个指针 front 和 rear 分别指向队列的头部和尾部。当 rear 指针到达数组末尾时，再次从数组头部开始存储元素，实现循环利用数组空间的效果。

不同实现方式适用的场景

数组实现队列、链表实现队列和循环队列实现，都有各自的特点和适用场景，以下是不同实现方式的一些适用场景：

  1. 数组实现适用于以下场景：

    • 队列大小固定，不需要频繁进行大小调整。
    • 元素个数相对较少，不会造成数组空间的浪费。
    • 需要快速随机访问队列元素。

  2. 链表实现适用于以下场景：

    • 队列大小不确定，会频繁进行大小调整。
    • 元素个数可能非常大，链表能够动态分配内存。
    • 需要频繁进行插入和删除操作。

  3. 循环队列实现适用于以下场景：

    • 队列大小固定，不需要频繁进行大小调整。
    • 队列元素个数可能会超过数组大小，但是可以接受覆盖旧元素的方式。
    • 需要快速入队和出队操作。

根据实际需求和对性能的要求，可以选择适合的实现方式。例如，如果队列大小固定且元素个数不会超过数组大小，可以选择数组实现；如果队列大小不确定且需要频繁进行插入和删除操作，可以选择链表实现；如果队列大小固定但元素个数可能超过数组大小且需要快速入队和出队操作，可以选择循环队列实现。

链表实现队列

定义基于链表的队列结构

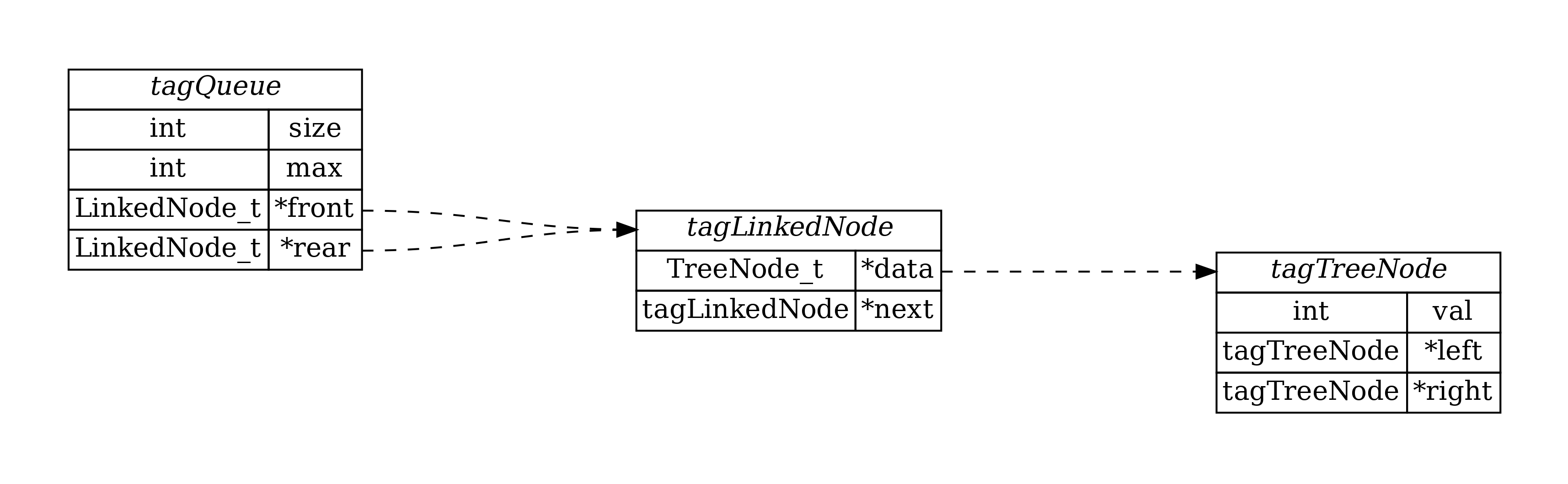
为了体现队列中数据的复杂性 ，这里不再使用基本数据类型（如整形、字符型）作为队列中的数据，而是使用了二叉树结构，即在队列中保存的数据是一个二叉树节点，节点中包含节点值、节点的左子树指针和节点的右子树指针。

FIFO 队列数据结构

首先，定义二叉树的结构：

1
2
3
4
5
6
// Definition for a binary tree node.
typedef struct tagTreeNode {
    int val;
    struct tagTreeNode *left;
    struct tagTreeNode *right;
} TreeNode_t;

然后，定义链表的结构：

1
2
3
4
5
// Define the structure for a node in the queue
typedef struct tagLinkedNode {
    TreeNode_t *data;
    struct tagLinkedNode *next;
} LinkedNode_t;

在这里，链表中的成员就是：用于存储二叉树节点数据的结构体和指向下一个链表节点的指针。

最后，定义队列的结构：

1
2
3
4
5
6
7
// Define the structure for the queue
typedef struct tagQueue {
    int size;
    int max;
    LinkedNode_t *front;
    LinkedNode_t *rear;
} Queue_t;

在这里，队列中的成员就是：队头指针和队尾指针，以及一个记录队列中数据数量的成员变量和一个标记队列可以容纳的最大数据量的成员变量。

队列的创建与初始化

首先，创建一个空队列（队列中还没有存储数据），并初始化成员变量。

1
2
3
4
5
6
7
8
9
// Function to create an empty queue
Queue_t *createQueue(int max_size) {
    Queue_t *queue = (Queue_t *)malloc(sizeof(Queue_t));
    queue->front = NULL;
    queue->rear = NULL;
    queue->size = 0;
    queue->max = max_size;
    return queue;
}

然后，对于空队列，后续入队操作会有数据存储到队列中，数据需要必要的存储空间来存储。在这里，我们创建并初始化一段空间用于存储数据。

1
2
3
4
5
6
7
// Function to create a new node
LinkedNode_t *createNode(TreeNode_t *data) {
    LinkedNode_t *newNode = (LinkedNode_t *)malloc(sizeof(LinkedNode_t));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

判断队列是否为空 

1
2
3
4
// Function to check if the queue is empty
bool isEmpty(Queue_t *queue) {
    return queue->size == 0;
}

当然，也可以使用 (!queue->front) && (queue->front == queue->rear) 判断队列是否为空。

判断队列是否已满 

1
2
3
4
// Function to check if the queue is full
bool isFull(Queue_t *queue) {
    return queue->size >= queue->max;
}

入队操作

入队操作，即在队列的尾部插入一个数据。

  • 如果队列已满，则无法继续执行入队操作；
  • 如果队列为空，则队列的头指针（front）和尾指针（rear）都指向新插入的数据的存放地址；
  • 否则，链接并更新队列的尾指针（rear）为新插入的数据的存放地址。

入队操作后需要更新队列的大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// Function to enqueue an element into the queue
void enQueue(Queue_t *queue, TreeNode_t *data) {
    if (isFull(queue)) {
        printf("queue is full.\n");
    } else {
        LinkedNode_t *newNode = createNode(data);
        if (isEmpty(queue)) {
            queue->front = queue->rear = newNode;
        } else {
            queue->rear->next = newNode;  // 尾指针链接新数据 
            queue->rear = newNode;  // 尾指针指向新数据 
        }
        queue->size += 1;  // 更新队列大小 
    }
}

出队操作

出队操作，即在队列的头部删除一个数据。出队操作需要依次执行以下操作：

  1. 获取头指针地址 & 数据；
  2. 更新队列头指针；
  3. 更新队列大小；
  4. 释放原头指针内存空间；
  5. 返回数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// Function to dequeue an element from the queue
TreeNode_t *deQueue(Queue_t* queue) {
    if (isEmpty(queue)) {
        return NULL;
    }
    LinkedNode_t *node = queue->front;
    TreeNode_t *data = node->data;
    // 根据当前队列中节点的数量，决定是否同步更新队列的尾指针 
    if (queue->size > 1) {
        queue->front = queue->front->next;
    } else {
        queue->front = queue->rear = NULL;
    }
    queue->size -= 1;
    free(node);
    return data;
}

Tips：出队操作在在更新队列头指针时，需要根据当前队列中节点的数量，决定是否同步更新队列的尾指针。

释放 node 内存空间后，不会造成 data 数据无法访问吗？
不会。这是因为，在释放节点之前，我们先将数据指针 node->data 保存到一个新的变量 data 中，然后释放节点，最后返回保存的数据指针。这样可以确保返回的数据指针依然有效。

打印队列数据 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Function to print all elements from the queue
void printQueue(Queue_t* queue) {
    if (isEmpty(queue)) {
        printf("Queue is empty\n");
    } else {
        printf("Queue: ");
        LinkedNode_t *node = queue->front;
        while (node != NULL) {
            printf("%d ", node->data->val);
            node = node->next;
        }
        printf("\n");
    }
}

释放队列 

1
2
3
4
5
6
7
8
9
10
11
12
// Function to free all memory from the queue
void freeQueue(Queue_t* queue) {
    if (queue) {
        LinkedNode_t *node = queue->front;
        while (node) {
            LinkedNode_t *temp = node;
            node = node->next;
            free(node);
        }
        free(queue);
    }
}

释放队列内存空间时，需要依次释放队列中的每一个节点的空间，最后再释放队列结构本身的数据空间。

链表实现队列完整代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct tagTreeNode {
    int val;
    struct tagTreeNode *left;
    struct tagTreeNode *right;
} TreeNode_t;

typedef struct tagLinkedNode {
    TreeNode_t *data;
    struct tagLinkedNode *next;
} LinkedNode_t;

typedef struct tagQueue {
    int size;
    int max;
    LinkedNode_t *front;
    LinkedNode_t *rear;
} Queue_t;

Queue_t *createQueue(int max_size) {
    Queue_t *queue = (Queue_t *)malloc(sizeof(Queue_t));
    queue->front = NULL;
    queue->rear = NULL;
    queue->size = 0;
    queue->max = max_size;
    return queue;
}

LinkedNode_t *createNode(TreeNode_t *data) {
    LinkedNode_t *newNode = (LinkedNode_t *)malloc(sizeof(LinkedNode_t));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

bool isEmpty(Queue_t *queue) {
    return queue->size == 0;
}

bool isFull(Queue_t *queue) {
    return queue->size >= queue->max;
}

void enQueue(Queue_t *queue, TreeNode_t *data) {
    if (isFull(queue)) {
        printf("queue is full.\n");
    } else {
        LinkedNode_t *newNode = createNode(data);
        if (isEmpty(queue)) {
            queue->front = queue->rear = newNode;
        } else {
            queue->rear->next = newNode;  // 尾指针链接新数据 
            queue->rear = newNode;  // 尾指针指向新数据 
        }
        queue->size += 1;  // 更新队列大小 
    }
}

TreeNode_t *deQueue(Queue_t* queue) {
    if (isEmpty(queue)) {
        return NULL;
    }
    LinkedNode_t *node = queue->front;
    TreeNode_t *data = node->data;
    // 根据当前队列中节点的数量，决定是否同步更新队列的尾指针 
    if (queue->size > 1) {
        queue->front = queue->front->next;
    } else {
        queue->front = queue->rear = NULL;
    }
    queue->size -= 1;
    free(node);
    return data;
}

void printQueue(Queue_t* queue) {
    if (isEmpty(queue)) {
        printf("Queue is empty\n");
    } else {
        printf("Queue: ");
        LinkedNode_t *node = queue->front;
        while (node != NULL) {
            printf("%d ", node->data->val);
            node = node->next;
        }
        printf("\n");
    }
}

void freeQueue(Queue_t* queue) {
    if (queue) {
        LinkedNode_t *node = queue->front;
        while (node) {
            LinkedNode_t *temp = node;
            node = node->next;
            free(node);
        }
        free(queue);
    }
}

int main(int argc, char *argv[]) {
    Queue_t *queue = createQueue(3);

    // 创建一些测试用的树节点 
    TreeNode_t *node = (TreeNode_t *)malloc(4 * sizeof(TreeNode_t));
    for (int i = 0; i < 4; ++i) {
        node[i].val = 10 + i;
        node[i].left = NULL;
        node[i].right = NULL;
    }

    printQueue(queue);

    enQueue(queue, &node[0]);
    enQueue(queue, &node[1]);
    enQueue(queue, &node[2]);
    printQueue(queue);

    enQueue(queue, &node[3]);
    printQueue(queue);

    TreeNode_t *data1 = deQueue(queue);
    TreeNode_t *data2 = deQueue(queue);
    TreeNode_t *data3 = deQueue(queue);
    printf("Dequeued data: %d %d %d\n", data1->val, data2->val, data3->val); // 实际工程中要先判非空再取数据 
    printQueue(queue);

    freeQueue(queue);
    free(node);

    return 0;
}

程序的输出结果为：

1
2
3
4
5
6
Queue is empty
Queue: 10 11 12
queue is full.
Queue: 10 11 12
Dequeued data: 10 11 12
Queue is empty
aha
2023-10-17
数据结构 队列
Expand all Back to top Go to bottom Search in blogs
银河白
豆沙绿
杏仁黄
青草绿
秋叶褐