AHA'S BOOK

二叉搜索树（Binary Search Tree，BST）是一种常见的数据结构，它具有以下特点：

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值。
  • 它的左、右子树也分别为二叉搜索树。

由于 BST 的特点，二叉搜索树的查找、插入和删除效率都很高（BST 足够「平衡」情况下）。

二叉搜索树操作

二叉搜索树是什么样子的呢？百闻不如一见，直接上图：

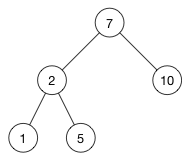
插入一个节点

如果我们插入一个节点，它的值为 9，我们应该插在哪里呢？看图~

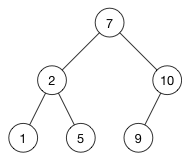
我们插入值 9 的过程大概是这样的：

  1. 9 > 根节点 7 吗？大于，则转向看右子树；
  2. 9 > 根节点 10 吗？小于，则转向看左子树；
  3. 左子树为空，则将 9 插入在这里。

看看，这是不是跟有序数组的二分查找算法的思想一样呢，根据值的大小关系，决定下次搜索的区域（但 BST 的判断不一定每次都会排除 50% 的区域，这要看 BST 是否足够「平衡」）！

搜索一个节点

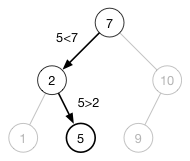
搜索一个节点的过程跟上面插入一个节点的过程类似：

  1. 5 == 根节点 7 吗？不等于；大于吗？小于，则转向左子树搜索；
  2. 5 == 根节点 2 吗？不等于；大于吗？大于，则转向右子树搜索；
  3. 5 == 根节点 5 吗？等于，搜索成功。

遍历二叉搜索树

我们知道，二叉树的遍历有前序遍历、中序遍历和后续遍历以及层序遍历。它们有不同的特点：

  • 前序遍历：先遍历根节点，再遍历左右子树；
  • 中序遍历：先遍历左子树，中间遍历根节点，最后遍历右子树；
  • 后续遍历：先遍历左子树和右子树，最后遍历根节点；
  • 层序遍历：从上到下、从左到右，按层遍历二叉树中的每一个节点。

结合二叉搜索树的特点：左子树上所有结点的值均小于它的根结点的值 & 右子树上所有结点的值均大于它的根结点的值。设想一下，如果我们先获取左子树的值，再获取根节点的值，最后再获取右子树的值，并将它们按获取顺序保存到数组中，那么这个数组是不是按升序排序的数组呢？

没错，二叉搜索树的中序遍历的结果是一个按升序排序的有序数组，所以二叉搜索树又称二叉排序树。

二叉搜索树的中序遍历过程图。

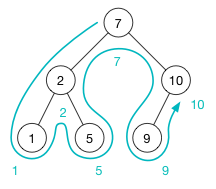
删除一个节点

删除节点也很容易，根据二叉搜索树的特点，我们删除一个节点后，只需要将这个节点的左子树的最大值（或者是右子树的最小值）拿过来，放到这个被删除的节点这里即可。这样，删除一个节点后，这棵树依然是一棵二叉搜索树。

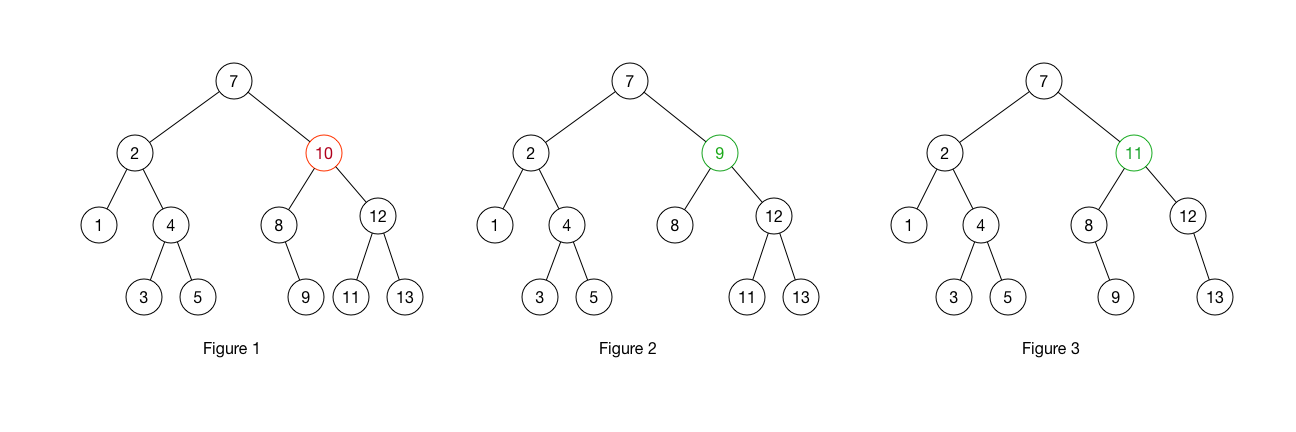
上图的 BST 删除一个节点中，Fig. 1 -> Fig. 2 使用了左子树的最大值，Fig. 1 -> Fig. 3 使用了右子树的最小值。

二叉搜索树接口实现

定义 BST 结构

BST 结构定义与普通二叉树结构定义没有区别。

1
2
3
4
5
typedef struct treeNode {
    int val;
    struct treeNode *left;
    struct treeNode *right;
} TreeNode_t;

创建一个节点

1
2
3
4
5
6
7
TreeNode_t* createNode(int val) {
    TreeNode_t *newNode = (TreeNode_t *)malloc(sizeof(TreeNode_t));
    newNode->val = val;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

插入一个节点（迭代实现）

给定一棵 BST，插入一个节点的过程为：

  1. 判断根节点是否为空：
    • 为空，则创建一个节点，并返回该节点。
  2. 根节点不为空，则判断插入的节点值与根节点的大小关系：
    • 相等，则不需插入，直接返回根节点。
    • 小于，则需要确定根节点是否有左子树：
      • 无左子树，则创建一个节点并将其作为根节点的左子树，插入节点结束。
      • 有左子树，更新根节点为左孩子节点，继续执行步骤 2；
    • 大于，则需要确定根节点是否有右子树：
      • 无右子树，则创建一个节点并将其作为根节点的右子树，插入节点结束。
      • 有右子树，更新根节点为右孩子节点，继续执行步骤 2；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
TreeNode_t* insertNode(TreeNode_t* root, int val) {
    if (root == NULL) {
        return createNode(val);
    }

    TreeNode_t *curNode = root;
    while (true) {
        if (curNode->val == val) {
            break;
        } else if (val < curNode->val) {
            if (curNode->left == NULL) {
                curNode->left = createNode(val);
                break;
            }
            curNode = curNode->left;
        } else {
            if (curNode->right == NULL) {
                curNode->right = createNode(val);
                break;
            }
            curNode = curNode->right;
        }
    }
    return root;
}

插入一个节点（递归实现）

通过插入节点的迭代实现可以看出，插入的过程本质上是插入的值与不同子树的根节点做大小比较的过程，并在合适的位置插入新节点。因此，我们也可以递归地实现插入节点。

1
2
3
4
5
6
7
8
9
10
TreeNode_t* insertNode(TreeNode_t* root, int val) {
    if (root == NULL) {
        return createNode(val);
    } else if (val < root->val) {
        root->left = insertNode(root->left, val);
    } else if (val > root->val) {
        root->right = insertNode(root->right, val);
    }
    return root;
}

搜索一个节点（迭代实现）

给定一棵 BST，搜素一个节点的过程为：

  1. 判断根节点是否为空：
    • 为空，则搜索失败，返回 NULL。
    • 不为空，判断值是否相等：
      • 相等，则搜索成功，返回当前节点。
      • 不相等，则判断搜索值与根节点值的大小关系，更新根节点，并重复步骤 1。
1
2
3
4
5
6
7
8
9
10
11
TreeNode_t* searchNode(TreeNode_t* root, int val) {
    TreeNode_t *curNode = root;
    while (curNode && (val != curNode->val)) {
        if (val < curNode->val) {
            curNode = curNode->left;
        } else {
            curNode = curNode->right;
        }
    }
    return curNode;
}

搜索一个节点（递归实现）

同样地，搜索一个节点也有递归实现方式。

1
2
3
4
5
6
7
8
9
TreeNode_t* searchNode(TreeNode_t* root, int val) {
    if (root == NULL || val == root->val) {
        return root;
    } else if (val < root->val) {
        return searchNode(root->left, val);
    } else {
        return searchNode(root->right, val);
    }
}

中序遍历 BST

就像上面说的，二叉搜索树的中序遍历的结果是一个按升序排序的有序数组。

1
2
3
4
5
6
7
void inOrderTraversal(TreeNode_t* root) {
    if (root) {
        inOrderTraversal(root->left);
        printf("%d ", root->val);
        inOrderTraversal(root->right);
    }
}

遍历也是递归实现？！二叉树的每一棵子树还是一棵二叉树，所以二叉树的很多操作都可以用递归的方式实现。

查找 BST 的最小节点

给定一棵 BST 或它的子树，有时需要查找它的最小节点（比如后面的删除一个节点时，就会用到这个函数哦）。

1
2
3
4
5
6
TreeNode_t* findMinNode(TreeNode_t* root) {
    while (root->left != NULL) {
        root = root->left;
    }
    return root;
}

查找 BST 的最大节点

给定一棵 BST 或它的子树，有时需要查找它的最大节点（比如后面的删除一个节点时，也可能用到这个函数哦）。

1
2
3
4
5
6
TreeNode_t* findMaxNode(TreeNode_t* root) {
    while (root->right != NULL) {
        root = root->right;
    }
    return root;
}

查找前驱节点

在 BST 中，一个节点的 前驱节点定义为比该节点小的所有节点中的最大节点。换句话说，它是在中序遍历顺序中位于该节点之前的节点。

如何确定前驱节点呢？

  • 如果一个节点有左子树，那么左子树的最大值就是前驱节点；
  • 如果一个节点没有左子树，那么它的前驱节点就是离它最近的拥有右子树的祖先节点；
    • 确定方法 ：从根节点搜，只要值比该节点的值小，它就 可能 是前驱节点。通过在满足条件的情况下，不断更新这个节点（离它越来越近），最后就是前驱节点啦。
  • 如果一个节点既没有左子树也没有右子树，那么它没有前驱节点。

什么叫「离它最近的拥有右子树的祖先节点」呢？
举个例子，上面的那张图中，节点 5 没有右子树，离它最近的拥有右子树的节点是节点 2，节点 2 是节点 5 的祖先节点，所以 5 的前驱节点是 2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
TreeNode_t* predecessorNode(TreeNode_t* root, TreeNode_t* node) {
    if (node == NULL)
        return NULL;

    // 如果节点有左子树，则前驱节点为左子树中的最右节点
    if (node->left) {
        return findMaxNode(node->left);
    }
    
    // 如果节点没有左子树，则前驱节点为离它最近的拥有右子树的祖先节点
    TreeNode_t* predecessor = NULL;
    while (root != NULL) {
        if (root->val < node->val) {
            predecessor = root;
            root = root->right;
        } else if (root->val > node->val) {
            root = root->left;
        } else {
            break;
        }
    }
    
    return predecessor;
}

参数一为 BST 的根节点，参数二为 BST 的某一节点，即想要查找参数二的前驱节点，参数二也可以传入根节点哦。

查找后驱节点

在 BST 中，一个节点的 后驱节点定义为比该节点大的所有节点中的最小节点。换句话说，它是在中序遍历顺序中位于该节点之后的节点。

如何确定后驱节点呢？

  • 如果一个节点有右子树，那么右子树的最小值就是后驱节点；
  • 如果一个节点没有右子树，那么它的后驱节点就是离它最近的拥有左子树的祖先节点；
  • 如果一个节点既没有右子树也没有左子树，那么它没有后驱节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
TreeNode_t* successorNode(TreeNode_t* root, TreeNode_t* node) {
    if (node == NULL)
        return NULL;

    // 如果节点有右子树，则后驱节点为右子树中的最左节点
    if (node->right) {
        return findMinNode(node->right);
    }
    
    // 如果节点没有右子树，则后驱节点为离它最近的拥有左子树的祖先节点
    TreeNode_t* successor = NULL;
    while (root != NULL) {
        if (root->val > node->val) {
            successor = root;
            root = root->left;
        } else if (root->val < node->val) {
            root = root->right;
        } else {
            break;
        }
    }
    
    return successor;
}

删除一个节点（递归实现）

给定一棵 BST，删除一个节点的思路为：

  • 若待删除的值小于根节点的值，则在左子树中查找并删除；
  • 若待删除的值大于根节点的值，则在右子树中查找并删除；
  • 若待删除的值等于根节点的值，要看它有没有左、右子树：
    • 无左子树和右子树：直接删除；
    • 仅有左子树，则只需更新根节点的地址为其左孩子的地址，并释放原根节点空间即可。
    • 仅有右子树，则只需更新根节点的地址为其右孩子的地址，并释放原根节点空间即可。
    • 既有左子树、又有右子树：
      • 找左子树的最大值节点, 将根节点的值替换它的值，并删除它（又一次调用删除一个节点的函数）；或者找右子树的最小值节点, 将根节点的值替换它的值，并删除它。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
TreeNode_t* deleteNode(TreeNode_t* root, int val) {
    if (root == NULL) {
        return root;
    } else if (val < root->val) {
        root->left = deleteNode(root->left, val);
    } else if (val > root->val) {
        root->right = deleteNode(root->right, val);
    } else {
        // 找到要删除的节点
        if (root->left == NULL && root->right == NULL) {
            // 没有子节点的情况
            free(root);
            root = NULL;
        } else if (root->left == NULL) {
            // 只有右子节点的情况
            TreeNode_t* temp = root;
            root = root->right;
            free(temp);
        } else if (root->right == NULL) {
            // 只有左子节点的情况
            TreeNode_t* temp = root;
            root = root->left;
            free(temp);
        } else {
            // 有两个子节点的情况
            // 找左子树的最大值, 替换并删除它; 或者找右子树的最小值, 替换并删除它
            TreeNode_t* temp = findMinNode(root->right);
            root->val = temp->val;
            root->right = deleteNode(root->right, temp->val);
        }
    }
    return root;
}

销毁 BST

1
2
3
4
5
6
7
void destroyBST(TreeNode_t* root) {
    if (root != NULL) {
        destroyBST(root->left);
        destroyBST(root->right);
        free(root);
    }
}

需要注意的是，在销毁二叉搜索树后，我们要将根节点指针 root 设为 NULL，以防止在后续操作中误用已被释放的内存。

1
2
destroyBST(root);
root = NULL;

BST 完整代码测试

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
typedef struct treeNode {
    int val;
    struct treeNode *left;
    struct treeNode *right;
} TreeNode_t;

TreeNode_t* createNode(int val) {
    TreeNode_t *newNode = (TreeNode_t *)malloc(sizeof(TreeNode_t));
    newNode->val = val;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

TreeNode_t* insertNode(TreeNode_t* root, int val) {
    if (root == NULL) {
        return createNode(val);
    } else if (val < root->val) {
        root->left = insertNode(root->left, val);
    } else if (val > root->val) {
        root->right = insertNode(root->right, val);
    }
    return root;
}

TreeNode_t* searchNode(TreeNode_t* root, int val) {
    if (root == NULL || val == root->val) {
        return root;
    } else if (val < root->val) {
        return searchNode(root->left, val);
    } else {
        return searchNode(root->right, val);
    }
}

void inOrderTraversal(TreeNode_t* root) {
    if (root) {
        inOrderTraversal(root->left);
        printf("%d ", root->val);
        inOrderTraversal(root->right);
    }
}

TreeNode_t* findMinNode(TreeNode_t* root) {
    while (root->left != NULL) {
        root = root->left;
    }
    return root;
}

TreeNode_t* findMaxNode(TreeNode_t* root) {
    while (root->right != NULL) {
        root = root->right;
    }
    return root;
}

TreeNode_t* predecessorNode(TreeNode_t* root, TreeNode_t* node) {
    if (node == NULL)
        return NULL;

    // 如果节点有左子树，则前驱节点为左子树中的最右节点
    if (node->left) {
        return findMaxNode(node->left);
    }
    
    // 如果节点没有左子树，则前驱节点为离它最近的拥有右子树的祖先节点
    TreeNode_t* predecessor = NULL;
    while (root != NULL) {
        if (root->val < node->val) {
            predecessor = root;
            root = root->right;
        } else if (root->val > node->val) {
            root = root->left;
        } else {
            break;
        }
    }
    
    return predecessor;
}

TreeNode_t* successorNode(TreeNode_t* root, TreeNode_t* node) {
    if (node == NULL)
        return NULL;

    // 如果节点有右子树，则后驱节点为右子树中的最左节点
    if (node->right) {
        return findMinNode(node->right);
    }
    
    // 如果节点没有右子树，则后驱节点为离它最近的拥有左子树的祖先节点
    TreeNode_t* successor = NULL;
    while (root != NULL) {
        if (root->val > node->val) {
            successor = root;
            root = root->left;
        } else if (root->val < node->val) {
            root = root->right;
        } else {
            break;
        }
    }
    
    return successor;
}

TreeNode_t* deleteNode(TreeNode_t* root, int val) {
    if (root == NULL) {
        return root;
    } else if (val < root->val) {
        root->left = deleteNode(root->left, val);
    } else if (val > root->val) {
        root->right = deleteNode(root->right, val);
    } else {
        // 找到要删除的节点
        if (root->left == NULL && root->right == NULL) {
            // 没有子节点的情况
            free(root);
            root = NULL;
        } else if (root->left == NULL) {
            // 只有右子节点的情况
            TreeNode_t* temp = root;
            root = root->right;
            free(temp);
        } else if (root->right == NULL) {
            // 只有左子节点的情况
            TreeNode_t* temp = root;
            root = root->left;
            free(temp);
        } else {
            // 有两个子节点的情况
            // 找左子树的最大值, 替换并删除它; 或者找右子树的最小值, 替换并删除它
            TreeNode_t* temp = findMinNode(root->right);
            root->val = temp->val;
            root->right = deleteNode(root->right, temp->val);
        }
    }
    return root;
}

void destroyBST(TreeNode_t* root) {
    if (root != NULL) {
        destroyBST(root->left);
        destroyBST(root->right);
        free(root);
    }
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>

// 规范化地打印二叉树
void printBinaryTree(TreeNode_t* root) {
    if (root == NULL) {
        return;
    }
    printf("(");
    printBinaryTree(root->left);
    printf(" <- %d -> ", root->val);
    printBinaryTree(root->right);
    printf(")");
}

int main(int argv, char *argc[]) {
    TreeNode_t* root = NULL;

    // 测试插入节点和搜索节点
    root = insertNode(root, 5);
    root = insertNode(root, 3);
    root = insertNode(root, 7);
    root = insertNode(root, 2);
    root = insertNode(root, 4);
    root = insertNode(root, 6);
    root = insertNode(root, 8);

    TreeNode_t* result = searchNode(root, 6);
    if (result != NULL) {
        printf("Node found: %d\n", result->val);
    } else {
        printf("Node not found\n");
    }

    result = searchNode(root, 9);
    if (result != NULL) {
        printf("Node found: %d\n", result->val);
    } else {
        printf("Node not found\n");
    }

    // 测试中序遍历
    printf("In-order traversal: ");
    inOrderTraversal(root);
    printf("\n");

    // 测试查找最小值节点和最大值节点
    TreeNode_t* minNode = findMinNode(root);
    printf("Minimum value: %d\n", minNode->val);

    TreeNode_t* maxNode = findMaxNode(root);
    printf("Maximum value: %d\n", maxNode->val);

    printBinaryTree(root);
    printf("\n");
    

    // 测试前驱节点和后继节点
    TreeNode_t* node = searchNode(root, 4);
    TreeNode_t* predecessor = predecessorNode(root, node);
    if (predecessor != NULL) {
        printf("Predecessor of %d: %d\n", node->val, predecessor->val);
    } else {
        printf("No predecessor for %d\n", node->val);
    }

    node = searchNode(root, 7);
    TreeNode_t* successor = successorNode(root, node);
    if (successor != NULL) {
        printf("Successor of %d: %d\n", node->val, successor->val);
    } else {
        printf("No successor for %d\n", node->val);
    }

    // 测试删除节点
    root = deleteNode(root, 3);

    // 再次中序遍历，检查删除是否成功
    printf("In-order traversal after deletion: ");
    inOrderTraversal(root);
    printf("\n");

    // 销毁二叉搜索树
    destroyBST(root);
    root = NULL;

    return 0;
}

测试结果

1
2
3
4
5
6
7
8
9
Node found: 6
Node not found
In-order traversal: 2 3 4 5 6 7 8
Minimum value: 2
Maximum value: 8
(((<- 2 ->) <- 3 -> (<- 4 ->)) <- 5 -> ((<- 6 ->) <- 7 -> (<- 8 ->)))
Predecessor of 4: 3
Successor of 7: 8
In-order traversal after deletion: 2 4 5 6 7 8

插入和搜索的迭代实现方式也验证了，没有问题。

建立的这棵树是这样子的：

1
2
3
4
5
6
       5
     /   \
    /     \
   3       7
 /   \   /   \
2     4 6     8

节点 4 的前驱节点是 3，节点 7 的后驱节点是 8，没有问题！

参考资料：

  1. BST in swift-algorithm-club
aha
2023-10-20
数据结构 二叉搜索树
Expand all Back to top Go to bottom Search in blogs
银河白
豆沙绿
杏仁黄
青草绿
秋叶褐